Chapter 1. Simple Horizontal Curves
CURVE POINTS
By studying this course the surveyor learns to locate points using angles and distances. In construction surveying, the surveyor must often establish the line of a curve for road layout or some other construction.
The surveyor can establish curves of short radius, usually less than one tape length, by holding one end of the tape at the center of the circle and swinging the tape in an arc, marking as many points as desired.
As the radius and length of curve increases, the tape becomes impractical, and the surveyor must use other methods. Measured angles and straight line distances are usually picked to locate selected points, known as stations, on the circumference of the arc.
TYPES OF HORIZONTAL CURVES
A curve may be simple, compound, reverse, or spiral (figure l). Compound and reverse curves are treated as a combination of two or more simple curves, whereas the spiral curve is based on a varying radius.

Simple
The simple curve is an arc of a circle. It is the most commonly used. The radius of the circle determines the “sharpness” or “flatness” of the curve. The larger the radius, the “flatter” the curve.
Compound
Surveyors often have to use a compound curve because of the terrain. This curve normally consists of two simple curves curving in the same direction and joined together.
Reverse
A reverse curve consists of two simple curves joined together but curving in opposite directions. For safety reasons, the surveyor should not use this curve unless absolutely necessary.
Spiral
The spiral is a curve with varying radius used on railroads and somemodern highways. It provides a transition from the tangent to a simple curve or between simple curves in a compound curve.
STATIONING
On route surveys, the surveyor numbers the stations forward from the beginning of the project. For example, 0+00 indicates the beginning of the project. The 15+52.96 would indicate a point 1,552.96 feet from the beginning. A full station is 100 feet or 30 meters, making 15+00 and 16+00 full stations. A plus station indicates a point between full stations. (15+52.96 is a plus station.) When using the metric system, the surveyor does not use the plus system of numbering stations. The station number simply becomes the distance from the beginning of the project.
ELEMENTS OF A SIMPLE CURVE
Figure 2 shows the elements of a simple curve. They are described as follows, and their abbreviations are given in parentheses.

Point of Intersection (PI)
The point of intersection marks the point where the back and forward tangents intersect. The surveyor indicates it as one of the stations on the preliminary traverse.
Intersecting Angle (I)
The intersecting angle is the deflection angle at the PI. The surveyor either computes its value from the preliminary traverse station angles or measures it in the field.
Radius (R)
The radius is the radius of the circle of which the curve is an arc.
Point of Curvature (PC)
The point of curvature is the point where the circular curve begins. The back tangent is tangent to the curve at this point.
Point of Tangency (PT)
The point of tangency is the end of the curve. The forward tangent is tangent to the curve at this point.
Length of Curve (L)
The length of curve is the distance from the PC to the PT measured along the curve.
Tangent Distance (T)
The tangent distance is the distance along the tangents from the PI to the PC or PT. These distances are equal on a simple curve.
Central Angle (�)
The central angle is the angle formed by two radii drawn from the center of the circle (0) to the PC and PT. The central angle is equal in value to the I angle.
Long Chord (LC)
The long chord is the chord from the PC to the PT.
External Distance (E)
The external distance is the distance from the PI to the midpoint of the curve. The external distance bisects the interior angle at the PI.
Middle Ordinate (M)
The middle ordinate is the distance from the midpoint of the curve to the midpoint of the long chord. The extension of the middle ordinate bisects the central angle.
Degree of Curve (D)
The degree of curve defines the “sharpness” or “flatness” of the curve (figure 3). There are two definitions commonly in use for degree of curve, the arc definition and the chord definition.

Arc definition. The arc definition states that the degree of curve (D) is the angle formed by two radii drawn from the center of the circle (point O, figure 3) to the ends of an arc 100 feet or 30.48 meters long. In this definition, the degree of curve and radius are inversely proportional using the following formula:

As the degree of curve increases, the radius decreases. It should be noted that for a given intersecting angle or central angle, when using the arc definition, all the elements of the curve are inversely proportioned to the degree of curve. This definition is primarily used by civilian engineers in highway construction.
English system. Substituting D = 1° and length of arc = 100 feet, we obtain

Metric system. In the metric system, using a 30.48-meter length of arc and substituting D = 1°, we obtain

Chord definition. The chord definition states that the degree of curve is the angle formed by two radii drawn from the center of the circle (point O, figure 3) to the ends of a chord 100 feet or 30.48 meters long. The radius is computed by the following formula:

The radius and the degree of curve are not inversely proportional even though, as in the arc definition, the larger the degree of curve the “sharper” the curve and the shorter the radius. The chord definition is used primarily on railroads in civilian practice and for both roads and railroads by the military.
English system. Substituting D = 1° and given Sin ½ 1 = 0.0087265355

Metric system. Using a chord 30.48 meters long, the surveyor computes R by the formula

Substituting D = 1° and given Sin ½ 1° = 0.0087265335, solve for R as follows:


Chords
On curves with long radii, it is impractical to stake the curve by locating the center of the circle and swinging the arc with a tape. The surveyor lays these curves out by staking the ends of a series of chords (figure 4). Since the ends of the chords lie on the circumference of the curve, the surveyor defines the arc in the field. The length of the chords varies with the degree of curve. To reduce the discrepancy between the arc distance and chord distance, the surveyor uses the following chord lengths:

The chord lengths above are the maximum distances in which the discrepancy between the arc length and chord length will fall within the allowable error for taping, which is 0.02 foot per 100 feet on most construction surveys. Depending upon the terrain and the needs of the project foremen, the surveyor may stake out the curve with shorter or longer chords than recommended.
Deflection Angles
The deflection angles are the angles between a tangent and the ends of the chords from the PC. The surveyor uses them to locate the direction in which the chords are to be laid out. The total of the deflection angles is always equal to one half of the I angle. This total serves as a check on the computed deflection angles.
SIMPLE CURVE FORMULAS
The following formulas are used in the computation of a simple curve. All of the formulas, except those noted, apply to both the arc and chord definitions.

L is the distance around the arc for the arc definition, or the distance along the chords for the chord definition.

In the following formulas, C equals the chord length and d equals the deflection angle. All the formulas are exact for the arc definition and approximate for the chord definition.

This formula gives an answer in degrees.

in the metric system. The answer will be in minutes.
SOLUTION OF A SIMPLE CURVE
To solve a simple curve, the surveyor must know three elements. The first two are the PI station value and the I angle. The third is the degree of curve, which is given in the project specifications or computed using one of the elements limited by the terrain (see section II). The surveyor normally determines the PI and I angle on the preliminary traverse for the road. This may also be done by tri-angulation when the PI is inaccessible.
Chord Definition
The six-place natural trigonometric functions from table A-1 were used in the example. When a calculator is used to obtain the trigonometric functions, the results may vary slightly. Assume that the following is known: PI = 18+00, I = 45, and D = 15°.
Chord Definition (Feet)

Chords. Since the degree of curve is 15 degrees, the chord length is 25 feet. The surveyor customarily places the first stake after the PC at a plus station divisible by the chord length. The surveyor stakes the centerline of the road at intervals of 10,25,50 or 100 feet between curves. Thus, the level party is not confused when profile levels are run on the centerline. The first stake after the PC for this curve will be at station 16+50. Therefore, the first chord length or subchord is 8.67 feet. Similarly, there will be a subchord at the end of the curve from station 19+25 to the PT. This subchord will be 16,33 feet. The surveyor designates the subchord at the beginning, C1 , and at the end, C2 (figure 2).
Deflection Angles. After the subchords have been determined, the surveyor computes the deflection angles using the formulas. Technically, the formulas for the arc definitions are not exact for the chord definition. However, when a one-minute instrument is used to stake the curve, the surveyor may use them for either definition. The deflection angles are

The number of full chords is computed by subtracting the first plus station divisible by the chord length from the last plus station divisible by the chord length and dividing the difference by the standard (std) chord length. Thus, we have (19+25 – 16+50)-25 equals 11 full chords. Since there are 11 chords of 25 feet, the sum of the deflection angles for 25- foot chords is 11 x 1°52.5’ = 20°37.5’.
The sum of d , d , and the deflections for the full chords is

The surveyor should note that the total of the deflection angles is equal to one half of the I angle. If the total deflection does not equal one half of I, a mistake has been made in the calculations. After the total deflection has been decided, the surveyor determines the angles for each station on the curve. In this step, they are rounded off to the smallest reading of the instrument to be used in the field. For this problem, the surveyor must assume that a one-minute instrument is to be used. The curve station deflection angles are listed on page 6.
Special Cases. The curve that is solved on page 6 had an I angle and degree of curve whose values were whole degrees. When the I angle and degree of curve consist of degrees and minutes, the procedure in solving the curve does not change, but the surveyor must take care in substituting these values into the formulas for length and deflection angles. For example, if I = 42° 15’ and D = 5° 37’, the surveyor must change the minutes in each angle to a decimal part of a degree, or D = 42.25000°, I = 5.61667°. To obtain the required accuracy, the surveyor should convert values to five decimal places.

An alternate method for computing the length is to convert the I angle and degree of curve to minutes; thus, 42° 15’ = 2,535 minutes and 5° 37’ = 337 minutes. Substituting into the length formula gives

This method gives an exact result. If the surveyor converts the minutes to a decimal part of a degree to the nearest five places, the same result is obtained.
Since the total of the deflection angles should be one half of the I angle, a problem arises when the I angle contains an odd number of minutes and the instrument used is a one- minute instrument. Since the surveyor normally stakes the PT prior to running the curve, the total deflection will be a check on the PT. Therefore, the surveyor should compute to the nearest 0.5 degree. If the total deflection checks to the nearest minute in the field, it can be considered correct.
Curve Tables
The surveyor can simplify the computation of simple curves by using tables. Table A-5 lists long chords, middle ordinates, externals, and tangents for a l-degree curve with a radius of 5,730 feet for various angles of intersection. Table A-6 lists the tangent, external distance corrections (chord definition) for various angles of intersection and degrees of curve.
Arc Definition. Since the degree of curve by arc definition is inversely proportional to the other functions of the curve, the values for a one-degree curve are divided by the degree of curve to obtain the element desired. For example, table A-5 lists the tangent distance and external distance for an I angle of 75 degrees to be 4,396.7 feet and 1,492.5 feet, respectively. Dividing by 15 degrees, the degree of curve, the surveyor obtains a tangent distance of 293.11 feet and an external distance of 99.50 feet.
Chord Definition. To convert these values to the chord definition, the surveyor uses the values in table A-5. From table A-6, a correction of 0.83 feet is obtained for the tangent distance and for the external distance, 0.29 feet.
The surveyor adds the corrections to the tangent distance and external distance obtained from table A-5. This gives a tangent distance of 293.94 feet and an external distance of 99.79 feet for the chord definition.
After the tangent and external distances are extracted from the tables, the surveyor computes the remainder of the curve.
COMPARISON OF ARC AND CHORD DEFINITIONS
Misunderstandings occur between surveyors in the field concerning the arc and chord definitions. It must be remembered that one definition is no better than the other.
Different Elements
Two different circles are involved in comparing two curves with the same degree of curve. The difference is that one is computed by the arc definition and the other by the chord definition. Since the two curves have different radii, the other elements are also different.
5,730-Foot Definition
Some engineers prefer to use a value of 5,730 feet for the radius of a l-degree curve, and the arc definition formulas. When compared with the pure arc method using 5,729.58, the 5,730 method produces
discrepancies of less than one part in 10,000 parts. This is much better than the accuracy of the measurements made in the field and is acceptable in all but the most extreme cases. Table A-5 is based on this definition.
CURVE LAYOUT
The following is the procedure to lay out a curve using a one-minute instrument with a horizontal circle that reads to the right. The values are the same as those used to demonstrate the solution of a simple curve.
Setting PC and PT
With the instrument at the PI, the instrumentman sights on the preceding PI and keeps the head tapeman on line while the tangent distance is measured. A stake is set on line and marked to show the PC and its station value.
The instrumentman now points the instrument on the forward PI, and the tangent distance is measured to set and mark a stake for the PT.
Laying Out Curve from PC
The procedure for laying out a curve from the PC is described as follows. Note that the procedure varies depending on whether the road curves to the left or to the right.
Road Curves to Right. The instrument is set up at the PC with the horizontal circle at 0°00’ on the PI.
- The angle to the PT is measured if the PT can be seen. This angle will equal one half of the I angle if the PC and PT are located properly.
- Without touching the lower motion, the first deflection angle, d1 (0° 39’), is set on the horizontal circle. The instrumentman keeps the head tapeman on line while the first subchord distance, C1 (8.67 feet), is measured from the PC to set and mark station 16+50.
- The instrumentman now sets the second deflection angle, d1+ dstd (2° 32’), on the horizontal circle. The tapemen measure the standard chord (25 feet) from the previously set station (16+50) while the instrument man keeps the head tapeman on line to set station 16+75.
- The succeeding stations are staked out in the same manner. If the work is done correctly, the last deflection angle will point on the PT, and the last distance will be the subchord length, C2 (16.33 feet), to the PT.
Road Curves to Left. As in the procedures noted, the instrument occupies the PC and is set at 0°00’ pointing on the PI.
- The angle is measured to the PT, if possible, and subtracted from 360 degrees. The result will equal one half the I angle if the PC and PT are positioned properly.
- The first deflection, dl (0° 39’), is subtracted from 360 degrees, and the remainder is set on the horizontal circle. The first subchord, Cl (8.67 feet), is measured from the PC, and a stake is set on line and marked for station 16+50.
- The remaining stations are set by continuing to subtract their deflection angles from 360 degrees and setting the results on the horizontal circles. The chord distances are measured from the previously set station.
- The last station set before the PT should be C2 (16.33 feet from the PT), and its deflection should equal the angle measured in (1) above plus the last deflection, d2 (1° 14’).
Laying Out Curve from Intermediate Setup
When it is impossible to stake the entire curve from the PC, the surveyor must use an adaptation of the above procedure.
- Stake out as many stations from the PC as possible.
- Move the instrument forward to any station on the curve.
- Pick another station already in place, and set the deflection angle for that station on the horizontal circle. Sight that station with the instruments telescope in the reverse position.
- Plunge the telescope, and set the remaining stations as if the instrument was set over the PC.
Laying Out Curve from PT
If a setup on the curve has been made and it is still impossible to set all the remaining stations due to some obstruction, the surveyor can “back in” the remainder of the curve from the PT. Although this procedure has been set up as a method to avoid obstructions, it is widely used for laying out curves. When using the “backing in method,” the surveyor sets approximately one half the curve stations from the PC and the remainder from the PT. With this method, any error in the curve is in its center where it is less noticeable.
Road Curves to Right. Occupy the PT, and sight the PI with one half of the I angle on the horizontal circle. The instrument is now oriented so that if the PC is sighted, the instrument will read 0°00’. The remaining stations can be set by using their deflections and chord distances from the PC or in their reverse order from the PT.
Road Curves to Left. Occupy the PT and sight the PI with 360 degrees minus one half of the I angle on the horizontal circle. The instrument should read 0° 00’ if the PC is sighted.
Set the remaining stations by using their deflections and chord distances as if computed from the PC or by computing the deflections in reverse order from the PT.
CHORD CORRECTIONS
Frequently, the surveyor must lay out curves more precisely than is possible by using the chord lengths previously described.

To eliminate the discrepancy between chord and arc lengths, the chords must be corrected using the values taken from the nomography in table A-11. This gives the corrections to be applied if the curve was computed by the arc definition.
Table A-10 gives the corrections to be applied if the curve was computed by the chord definition. The surveyor should recall that the length of a curve computed by the chord definition was the length along the chords. Figure 5 illustrates the example given in table A-9. The chord distance from station 18+00 to station 19+00 is 100 feet. The nominal length of the subchords is 50 feet. Tables A-9, A-10 and A-11 from FM 5-233, are available on the PDH website.
INTERMEDIATE STAKE
If the surveyor desires to place a stake at station 18+50, a correction must be applied to the chords, since the distance from 18+00 through 18+50 to 19+00 is greater than the chord from 18+00 to 19+00. Therefore, a correction must be applied to the subchords to keep station 19+00 100 feet from 18+00. In figure 5, if the chord length is nominally 50 feet, then the correction is 0.19 feet. The chord distance from 18+00 to 18+50 and 18+50 to 19+00 would be 50.19.
Chapter 2. Obstacles To Curve Location
TERRAIN RESTRICTIONS
To solve a simple curve, the surveyor must know three parts. Normally, these will be the PI, I angle, and degree of curve. Sometimes, however, the terrain features limit the size of various elements of the curve. If this happens, the surveyor must determine the degree of curve from the limiting factor.
Inaccessible PI
 Under certain conditions, it may be impossible or impractical to occupy the PI. In this case, the surveyor locates the curve elements by using the following steps (figure 6).
Under certain conditions, it may be impossible or impractical to occupy the PI. In this case, the surveyor locates the curve elements by using the following steps (figure 6).
- Mark two intervisible points A and B, one on each of the tangents, so that line AB (a random line connecting the tangents) will clear the obstruction.
- Measure angles a and b by setting up at both A and B.
- Measure the distance AB.
- Compute inaccessible distances AV and BV as follows:
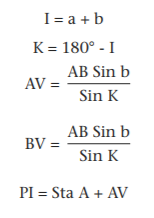
- Determine the tangent distance from the PI to the PC on the basis of the degree of curve or other given limiting factor.
- Locate the PC at a distance T minus AV from the point A and the PT at distance T minus BV from point B.
- Proceed with the curve computation and layout.
Inaccessible PC
 When the PC is inaccessible, as illustrated in figure 7, and both the PI and PT are set and readily accessible, the surveyor must establish the location of an offset station at the PC.
When the PC is inaccessible, as illustrated in figure 7, and both the PI and PT are set and readily accessible, the surveyor must establish the location of an offset station at the PC.
- Place the instrument on the PT and back the curve in as far as possible.
- Select one of the stations (for example, “P”) on the curve, so that a line PQ, parallel to the tangent line AV, will clear the obstacle at the PC.
- Compute and record the length of line PW so that point W is on the tangent line AV and line PW is perpendicular to the tangent. The length of line PW = R (l – Cos dp), where dp is that portion of the central angle subtended by AP and equal to two times the deflection angle of P.
- Establish point W on the tangent line by setting the instrument at the PI and laying off angle V (V = 180° – I). This sights the instrument along the tangent Swing a tape using the computed length of line PW and the line of sight to set point W.
- Measure and record the length of line VW along the tangent.
- Place the instrument at point P. Backsight point W and lay off a 90-degree angle to sight along line PQ, parallel to AV.
- Measure along this line of sight to a point Q beyond the obstacle. Set point Q, and record the distance PQ.
- Place the instrument at point Q, backsight P, and lay off a 90-degree angle to sight along line QS. Measure, along this line of sight, a distance QS equals PW, and set point S. Note that the station number of point S = PI – (line VW + line PQ).
- Set an offset PC at point Y by measuring from point Q toward point P a distance equal to the station of the PC minus station S. To set the PC after the obstacle has been removed, place the instrument at point Y, backsight point Q, lay off a 90-degree angle and a distance from Y to the PC equal to line PW and QS. Carefully set reference points for points Q, S, Y, and W to insure points are available to set the PC after clearing and construction have begun.
Inaccessible PT
 When the PT is inaccessible, as illustrated in figure 8, and both the PI and PC are readily accessible, the surveyor must establish an offset station at the PT using the method for inaccessible PC with the following exceptions.
When the PT is inaccessible, as illustrated in figure 8, and both the PI and PC are readily accessible, the surveyor must establish an offset station at the PT using the method for inaccessible PC with the following exceptions.
- Letter the curve so that point A is at the PT instead of the PC (see figure 8).
- Lay the curve in as far as possible from the PC instead of the PT.
- Angle dp is the angle at the center of the curve between point P and the PT, which is equal to two times the difference between the deflection at P and one half of I. Follow the steps for inaccessible PC to set lines PQ and QS. Note that the station at point S equals the computed station value of PT plus YQ.
- Use station S to number the stations of the alignment ahead.
Obstacle on Curve
Some curves have obstacles large enough to interfere with the line of sight and taping. Normally, only a few stations are affected. The surveyor should not waste too much time on preliminary work. Figure 9 illustrates a method of bypassing an obstacle on a curve.
- Set the instrument over the PC with the horizontal circle at 0˚ 00’, and sight on the Check I/2 from the PI to the PT, if possible.
- Set as many stations on the curve as possible before the obstacle, point b.
- Set the instrument over the PT with the plates at the value of I/2. Sight on the PI.
- Back in as many stations as possible beyond the obstacle, point e.
- After the obstacle is removed, the obstructed stations c and d can be set.
CURVE THROUGH FIXED POINT
 Because of topographic features or other obstacles, the surveyor may find it necessary to determine the radius of a curve which will pass through or avoid a fixed point and connect two given tangents. This may be accomplished as follows (figure 10):
Because of topographic features or other obstacles, the surveyor may find it necessary to determine the radius of a curve which will pass through or avoid a fixed point and connect two given tangents. This may be accomplished as follows (figure 10):
- Given the PI and the I angle from the preliminary traverse, place the instrument on the PI and measure angle d, so that angle d is the angle between the fixed point and the tangent line that lies on the same side of the curve as the fixed point.
- Measure line y, the distance from the PI to the fixed point.
- Compute angles c, b, and a in triangle COP.
c = 90 – (d + I/2)
To find angle b, first solve for angle e
Sin e = Sin c/Cos I/2
Angle b = 180°- angle e
a = 180° – (b + c) - Compute the radius of the desired curve using the formula
R = y Sin c/Sin a - Compute the degree of curve to five decimal places, using the following formulas:
(arc method) D = 5,729.58 ft/R D = 1,746.385 meters/R
(chord method) Sin D = 2 (50 feet/R) Sin D = 2 (15.24 meters/R) - Compute the remaining elements of the curve and the deflection angles, and stake the curve.
LIMITING FACTORS
In some cases, the surveyor may have to use elements other than the radius as the limiting factor in determining the size of the curve. These are usually the tangent T, external E, or middle ordinate M. When any limiting factor is given, it will usually be presented in the form of T equals some value x, T ≥ x or T ≤ x. In any case, the first step is to determine the radius using one of the following formulas:
Given: Tangent; then R = T/(Tan ½I)
External; then R = E/[(l/Cos ½I) – 1]
Middle Ordinate; then R = M/(l – Cos ½I)
The surveyor next determines D. If the limiting factor is presented in the form T equals some value x, the surveyor must compute D, hold to five decimal places, and compute the remainder of the curve. If the limiting factor is presented ≥, then D is rounded down to the nearest ½ degree. For example, if E ≥ 50 feet, the surveyor would round down to the nearest ½ degree, recompute E, and compute the rest of the curve data using the rounded value of D, The new value of E will be equal to or greater than 50 feet.
If the limiting factor is ≤ the D is rounded to the nearest ½ degree. For example, if M ≤ 45 feet, then D would be rounded up to the nearest ½ degree, M would be recomputed, and the rest of the curve data computed using the rounded value of D. The new value of M will be equal to or less than 45 feet.
The surveyor may also use the values from table A-5 to compute the value of D. This is done by dividing the tabulated value of tangent, external, or middle ordinate for a l-degree curve by the given value of the limiting factor. For example, given a limiting tangent T ≤ 45 feet and I = 20°20’, the T for a l-degree curve from table A-5 is 1,027.6 and D = 1,027.6/45.00 = 22.836°. Rounded up to the nearest half degree, D = 23°. Use this rounded value to recompute D, T and the rest of the curve data.
Chapter 3. Compound and Reverse Curves
COMPOUND CURVES
A compound curve is two or more simple curves which have different centers, bend in the same direction,
lie on the same side of their common tangent, and connect to form a continuous arc. The point where the two curves connect (namely, the point at which the PT of the first curve equals the PC of the second curve) is referred to as the point of compound curvature (PCC).
Since their tangent lengths vary, compound curves fit the topography much better than simple curves. These curves easily adapt to mountainous terrain or areas cut by large, winding rivers. However, since compound curves are more hazardous than simple curves, they should never be used where a simple curve will do.
Compound Curve Data
The computation of compound curves presents two basic problems. The first is where the compound curve is to be laid out between two successive PIs on the preliminary traverse. The second is where the curve is to be laid in between two successive tangents on the preliminary traverse. (See figure 11.)
Compound Curve between Successive PIs
 The calculations and procedure for laying out a compound curve between successive PIs are outlined in the following steps. This procedure is illustrated in figure 11a.
The calculations and procedure for laying out a compound curve between successive PIs are outlined in the following steps. This procedure is illustrated in figure 11a.
- Determine the PI of the first curve at point A from field data or previous computations.
- Obtain I1, I2, and distance AB from the field data.
- Determine the value of D1, the D for the first curve. This may be computed from a limiting factor based on a scaled value from the road plan or furnished by the project engineer.
- Compute R1, the radius of the first curve as shown on pages 11 through 13.
- Compute T1, the tangent of the first curve.
T1 = R1(Tan ½ I) - Compute T2, the tangent of the second curve.
T2 = AB – T1 - Compute R2, the radius of the second curve.
R2 =T2/Tan ½ I - Compute D2 for the second curve. Since the tangent for the second curve must be held exact, the value of D2 must be carried to five decimal places.
- Compare D1 and D2. They should not differ by more than 3 degrees, If they vary by more than 3 degrees, the surveyor should consider changing the configuration of the curve.
- If the two Ds are acceptable, then compute the remaining data and deflection angles for the first curve.
- Compute the PI of the second curve. Since the PCC is at the same station as the PT of the first curve, then PI2 = PT1 + T2.
- Compute the remaining data and deflection angles for the second curve, and lay in the curves.
Compound Curve between Successive Tangents. The following steps explain the laying out of a compound curve between successive tangents. This procedure is illustrated in figure llb.
- Determine the PI and I angle from the field data and/or previous computations.
- Determine the value of I1 and distance AB. The surveyor may do this by field measurements or by scaling the distance and angle from the plan and profile sheet.
- Compute angle C.
C = 180 – I - Compute I2.
I2 =180-(Il+C) - Compute line AC.
AC = AB Sin I2/Sin C - Compute line BC.
BC = AB Sin I1/Sin C - Compute the station of PI1.
PI1 = PI – AC - Determine D1 and compute R1 and T1 for the first curve as described on pages 11 through 13.
- Compute T2 and R2 as described onpages 11 through 13.
- Compute D2 according to the formulas on pages 11 through 13.
- Compute the station at PC.
PC1 = PI – (AC + T1) - Compute the remaining curve data and deflection angles for the first curve.
- Compute PI2.
PI2 = PT1 + T2 - Compute the remaining curve data and deflection angles for the second curve, and stake out the curves.
Staking Compound Curves
Care must be taken when staking a curve in the field. Two procedures for staking compound curves are described.
Compound Curve between Successive PIs. Stake the first curve as described on pages 14 and 15.
- Verify the PCC and PT2 by placing the instrument on the PCC, sighting on PI2, and laying off I2/2. The resulting line-of-sight should intercept PT2.
- Stake the second curve in the same manner as the first.
Compound Curve between Successive Tangents. Place the instrument at the PI and sight along the back tangent.
- Lay out a distance AC from the PI along the back tangent, and set PI1.
- Continue along the back tangent from PI2 a distance T1, and set PC1.
- Sight along the forward tangent with the instrument still at the PI.
- Lay out a distance BC from the PI along the forward tangent, and set PI2.
- Continue along the forward tangent from PI a distance T2, and set PT2.
- Check the location of PI1 and PI2 by either measuring the distance between the two PIs and comparing the measured distance to the computed length of line AB, or by placing the instrument at PI1, sighting the PI, and laying off I1. The resulting line-of-sight should intercept PI2.
- Stake the curves as outlined on pages 14 and 15.
REVERSE CURVES
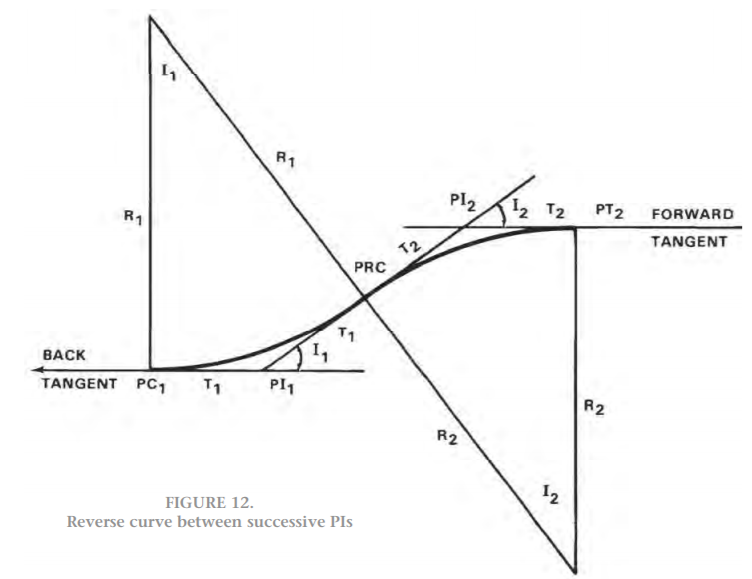
A reverse curve is composed of two or more simple curves turning in opposite directions. Their points of intersection lie on opposite ends of a common tangent, and the PT of the first curve is coincident with the PC of the second. This point is called the point of reverse curvature (PRC).
Reverse curves are useful when laying out such things as pipelines, flumes, and levees. The surveyor may also use them on low-speed roads and railroads. They cannot be used on high-speed roads or railroads since they cannot be properly superelevated at the PRC. They are sometimes used on canals, but only with extreme caution, since they make the canal difficult to navigate and contribute to erosion.
 Reverse Curve Data
Reverse Curve Data
The computation of reverse curves presents three basic problems. The first is where the reverse curve is to be laid out between two successive PIs. (See figure 12.) In this case, the surveyor performs the computations in exactly the same manner as a compound curve between successive PIs. The second is where the curve is to be laid out so it connects two parallel tangents (figure 13). The third problem is where the reverse curve is to be laid out so that it connects diverging tangents (figure 14).
Connecting Parallel Tangents
Figure 13 illustrates a reverse curve connecting two parallel tangents. The PC and PT are located as follows.
- Measure p, the perpendicular distance between tangents.
- Locate the PRC and measure m1 and m2. (If conditions permit, the PRC can be at the midpoint between the two tangents. This will reduce computation, since both arcs will be identical.)
- Determine R1.
- Compute I1.
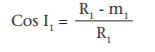
- Compute L1 from
L1 = R1 Sin I1
R2 ,I2 ,and L2 are determined in the same way as R1, I1, and L1. If the PRC is to be the midpoint, the values for arc 2 will be the same as for arc 1. - Stake each of the arcs the same as a simple curve. If necessary, the surveyor can easily determine other curve components. For example, the surveyor needs a reverse curve to connect two parallel tangents. No obstructions exist so it can be made up of two equal arcs. The degree of curve for both must be 5°. The surveyor measures the distance p and finds it to be 225.00 feet.
m1 = m2 and L1= L2 R1= R2 and I1= I2

- The PC and PT are located by measuring off L1and L2.
Connecting Diverging Tangents
The connection of two diverging tangents by a reverse curve is illustrated in figure 14. Due to possible obstruction or topographic consideration, one simple curve could not be used between the tangents. The PT has been moved back beyond the PI. However, the I angle still exists as in a simple curve. The controlling dimensions in this curve are the distance Ts to locate the PT and the values of R1 and R2, which are computed from the specified degree of curve for each arc.
- Measure I at the PI.
- Measure Ts to locate the PT as the point where the curve is to join the forward tangent. In some cases, the PT position will be specified, but Ts must still be measured for the computations.
- Perform the following calculations:
Determine R and R . If practical, have R equal R .
Angle s = 180-(90+I)=90-I
m = Ts (Tan I)
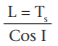
angle e = I1 (by similar triangles) angle f = I1 (by similar triangles) therefore, I2 = I + I1
n = (R2 – m) Sin e p = (R2 – m) Cos e
Determine g by establishing the value of I1.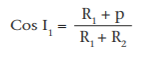 Knowing Cos I1, determine Sin I1.
Knowing Cos I1, determine Sin I1.
g = (R1+ R2) Sin I1
TL = g + n + L - Measure TL from the PI to locate the PC.
- Stake arc 1 to PRC from PC.
- Set instrument at the PT and verify the PRC (invert the telescope, sight on PI, plunge, and turn angle I2/2).
- Stake arc 2 to the PRC from PT.
For example, in figure 14, a reverse curve is to connect two diverging tangents with both arcs having a 5-degree curve. The surveyor locates the PI and measures the I angle as 41 degrees. The PT location is specified and the Ts is measured as 550 feet.


The PC is located by measuring T . The curve is staked using 5-degree curve computations.
Chapter 4. Transition Spirals
SPIRAL CURVES
In engineering construction, the surveyor often inserts a transition curve, also known as a spiral curve, between a circular curve and the tangent to that curve. The spiral is a curve of varying radius used to gradually increase the curvature of a road or railroad. Spiral curves are used primarily to reduce skidding and steering difficulties by gradual transition between straight-line and turning motion, and/or to provide a method for adequately superelevating curves.
The spiral curve is designed to provide for a gradual superelevation of the outer pavement edge of the road to counteract the centrifugal force of vehicles as they pass. The best spiral curve is one in which the superelevation increases uniformly with the length of the spiral from the TS or the point where the spiral curve leaves the tangent.
The curvature of a spiral must increase uniformly from its beginning to its end. At the beginning, where it leaves the tangent, its curvature is zero; at the end, where it joins the circular curve, it has the same degree of curvature as the circular curve it intercepts.
Theory of A.R.E.A. 10-Chord Spiral
The spiral of the American Railway Engineering Association, known as the A.R.E.A. spiral, retains nearly all the characteristics of the cubic spiral. In the cubic spiral, the lengths have been considered as measured along the spiral curve itself, but measurements in the field must be taken by chords. Recognizing this fact, in the A.R.E.A. spiral the length of spiral is measured by 10 equal chords, so that the theoretical curve
is brought into harmony with field practice. This 10-chord spiral closely approximates the cubic spiral. Basically, the two curves coincide up to the point where Δ = 15 degrees. The exact formulas for this A.R.E.A. 10-chord spiral, when Δ does not exeed 45 degrees, are given on pages 28 and 29.
Spiral Elements
 Figures 15 and 16 show the notations applied to elements of a simple circular curve with spirals connecting it to the tangents.
Figures 15 and 16 show the notations applied to elements of a simple circular curve with spirals connecting it to the tangents.
TS = the point of change from tangent to spiral
SC = the point of change from spiral to circular curve CS = the point of change from circular curve to spiral ST = the point of change from spiral to tangent
SS = the point of change from one spiral to another (not shown in figure 15 or figure 16)
The symbols PC and PT, TS and ST, and SC and CS become transposed when the direction of stationing is changed.
a = the angle between the tangent at the TS and the chord from the TS to any point on the spiral
A = the angle between the tangent at the TS and the chord from the TS to the SC
b = the angle at any point on the spiral between the tangent at that point and the chord from the TS
B = the angle at the SC between the chord from the TS and the tangent at the SC
c = the chord from any point on the spiral to the TS C = the chord from the TS to the SC
d = the degree of curve at any point on the spiral D = the degree of curve of the circular arc
f = the angle between any chord of the spiral (calculated when necessary) and the tangent through the TS
I = the angle of the deflection between initial and final tangents; the total central angle of the circular curve and spirals
k = the increase in degree of curve per station on the spiral
L = the length of the spiral in feet from the TS to any given point on the spiral
Ls = the length of the spiral in feet from the TS to the SC, measured in 10 equal chords
o = the ordinate of the offsetted PC; the distance between the tangent and a parallel tangent to the offsetted curve
r = the radius of the osculating circle at any given point of the spiral
R = the radius of the central circular curve
s = the length of the spiral in stations from the TS to any given point
S = the length of the spiral in stations from the TS to the SC
u = the distance on the tangent from the TS to the intersection with a tangent through any given point on the spiral
U = the distance on the tangent from the TS to the intersection with a tangent through the SC; the longer spiral tangent
v = the distance on the tangent through any given point from that point to the intersection with the tangent through the TS
V = the distance on the tangent through the SC from the SC to the intersection with the tangent through the TS; the shorter spiral tangent
x = the tangent distance from the TS to any point on the spiral
X = the tangent distance from the TS to the SC y = the tangent offset of any point on the spiral Y = the tangent offset of the SC
Z = the tangent distance from the TS to the offsetted PC (Z = X/2, approximately)
8 = the central angle of the spiral from the TS to any given point
Δ = the central angle of the whole spiral
Ts = the tangent distance of the spiraled curve; distance from TS to PI, the point of intersection of tangents
Es = the external distance of the offsetted curve
Spiral Formulas
The following formulas are for the exact determination of the functions of the 10- chord spiral when the central angle, Δ, does not exceed 45 degrees. These are suitable for the compilation of tables and for accurate fieldwork.


Empirical Formulas
For use in the field, the following formulas are sufficiently accurate for practical purposes when Δ does not exceed 15 degrees.
a = o/3 (degrees)
A = Δ/3 (degrees)
a = 10 ks2 (minutes)
S = 10 kS2(minutes)
Spiral Lengths
Different factors must be taken into account when calculating spiral lengths for highway and railroad layout.
 Highways. Spirals applied to highway layout must
Highways. Spirals applied to highway layout must
be long enough to permit the effects of centrifugal force to be adequately compensated for by proper superelevation. The minimum transition spiral length for any degree of curvature and design speed is obtained from the the relationship Ls= 1.6V3/R, in which Ls is the minimum spiral length in feet, V is the design speed in miles per hour, and R is the radius of curvature of the simple curve. This equation is not mathematically exact but an approximation based on years of observation and road tests.
Table 1 is compiled from the above equation for multiples of 50 feet. When spirals are inserted between the arcs of a compound curve, use Ls= 1.6V3/Ra. Ra represents the radius of a curve of a degree equal to the difference in degrees of curvature of the circular arcs.
Railroads Spirals applied to railroad layout must be long enough to permit an increase in superelevation not exceeding 1¼ inches per second for the maximum speed of train operation. The minimum length is determined from the equation Ls= 1.17 EV. E is the full theoretical superelevation of the curve in inches, V is the speed in miles per hour, and Ls is the spiral length in feet.
This length of spiral provides the best riding conditions by maintaining the desired relationship between the amount of superelevation and the degree of curvature. The degree of curvature increases uniformly throughout the length of the spiral. The same equation is used to compute the length of a spiral between the arcs of a compound curve. In such a case, E is the difference between the superelevations of the two circular arcs.
SPIRAL CALCULATIONS
Spiral elements are readily computed from the formulas given on pages 26 and 27. To use these formulas, certain data must be known. These data are normally obtained from location plans or by field measurements.
The following computations are for a spiral when D, V, PI station, and I are known.
D = 4°
I = 24°10’
PI station = 42 + 61.70
V = 60 mph
Determining Ls
- Assuming that this is a highway spiral, use either the equation on page 21 or table 1.
- From table 1, when D = 4° and V = 60 mph, the value for Ls is 250 feet.
Determining Δ

Determining o

Determining Z

Determining Ts

Determining Chord Length

Determining Station Values
With the data above, the curve points are calculated as follows:

Determining Deflection Angles
One of the principal characteristics of the spiral is that the deflection angles vary as the square of the distance along the curve.

From this equation, the following relationships are obtained:

The deflection angles to the various points on the spiral from the TS or ST are a1, a2, a3 . . . a9 and a10. Using these relationships, the deflection angles for the spirals and the circular arc are computed for the example spiral curve.
Page 21 states that.


SPIRAL CURVE LAYOUT
 The following is the procedure to lay out a spiral curve, using a one-minute instrument with a horizontal circle that reads to the right. Figure 17 illustrates this procedure.
The following is the procedure to lay out a spiral curve, using a one-minute instrument with a horizontal circle that reads to the right. Figure 17 illustrates this procedure.
Setting TS and ST
With the instrument at the PI, the instrumentman sights along the back tangent and keeps the head tapeman on line while the tangent distance (Ts) is measured. A stake is set on line and marked to show the TS and its station value.
The instrumentman now sights along the forward tangent to measure and set the ST.
Laying Out First Spiral from TS to SC
Set up the instrument at the TS, pointing on the PI, with 0°00’ on the horizontal circle.
- Check the angle to the ST, if possible. The angle should equal one half of the I angle if the TS and ST are located properly.
- The first deflection (a1/ 0˚ 01’) is subtracted from 360 degrees, and the remainder is set on the horizontal circle. Measure the standard spiral chord length (25 feet) from the TS, and set the first spiral station (38 + 54.66) on line.
- The remaining spiral stations are set by subtracting their deflection angles from 360 degrees and measuring 25 feet from the previously set station.
Laying Out Circular Arc from SC to CS
Set up the instrument at the SC with a value of A minus A (5° 00’- 1°40’ = 3° 20’) on the horizontal circle. Sight the TS with the instrument telescope in the reverse position.
- Plunge the telescope. Rotate the telescope until 0° 00’ is read on the horizontal circle. The instrument is now sighted along the tangent to the circular arc at the SC.
- The first deflection (dl /0° 24’) is subtracted from 360 degrees, and the remainder is set on the horizontal circle. The first subchord (c1 / 20.34 feet) is measured from the SC, and a stake is set on line and marked for station 41+00.
- The remaining circular arc stations are set by subtracting their deflection angles from 360 degrees and measuring the corresponding chord distance from the previously set station.
Laying Out Second Spiral from ST to CS
Set up the instrument at the ST, pointing on the PI, with 0° 00’ on the horizontal circle.
- Check the angle to the CS. The angle should equal 1° 40’ if the CS is located properly.
- Set the spiral stations using their deflection angles in reverse order and the standard spiral chord length (25 feet).
Correct any error encountered by adjusting the circular arc chords from the SC to the CS.
Intermediate Setup
When the instrument must be moved to an intermediate point on the spiral, the deflection angles computed from the TS cannot be used for the remainder of the spiral. In this respect, a spiral differs from a circular curve.
Calculating Deflection Angles Following are the procedures for calculating the deflection angles and staking the spiral.
Example:
D= 4°
Ls = 250 ft (for highways)
V =60 mph
I = 24° 10’
Point 5 = intermediate point
- Calculate the deflection angles for the first five points. These angles are: a1 = 0° 01’, a2 = 0˚ 04’, a3 = 0˚ 09’, a4 = 0° 16’, and a5 = 0° 25’.
- The deflection angles for points 6, 7, 8, 9, and 10, with the instrument at point 5, are calculated with the use of table 2. Table 2 is read as follows: with the instrument at any point, coefficients are obtained which, when multiplied by a1, give the deflection angles to the other points of the spiral. Therefore, with the instrument at point 5, the coefficients for points 6, 7, 8, 9, and 10 are 16, 34, 54, 76, and 100, respectively.
Multiply these coefficients by a1 to obtain the
Chapter 5. Vertical Curves
FUNCTION AND TYPES
When two grade lines intersect, there is a vertical change of direction. To insure safe and comfortable travel, the surveyor rounds off the intersection by inserting a vertical parabolic curve. The parabolic curve provides a gradual direction change from one grade to the next.
A vertical curve connecting a descending grade with an ascending grade, or with one descending less sharply, is called a sag or invert curve. An ascending grade followed by a descending grade, or one ascending less sharply, is joined by a summit or overt curve.
COMPUTATIONS
In order to achieve a smooth change of direction when laying out vertical curves, the grade must be brought up through a series of elevations. The surveyor normally determines elevation for vertical curves for the beginning (point of vertical curvature or PVC), the end (point of vertical tangency or PVT), and all full stations. At times, the surveyor may desire additional points, but this will depend on construction requirements.
Length of Curve
The elevations are vertical offsets to the tangent and (straightline design grade) elevations. Grades G1 G2 are given as percentages of rise for 100 feet of horizontal distance. The surveyor identifies grades as plus or minus, depending on whether they are ascending or descending in the direction of the survey. The length of the vertical curve (L) is the horizontal distance (in 100-foot stations) from PVC to PVT. Usually, the curve extends ½ L stations on each side of the point of vertical intersection (PVI) and is most conveniently divided into full station increments.
A sag curve is illustrated in figure 20. The surveyor can derive the curve data as follows (with BV and CV being the grade lines to be connected).
Determine values of G1 and G2, the original grades. To arrive at the minimum curve length (L) in stations, divide the algebraic difference of G1and G2 (AG) by the rate of change (r), which is normally included in the design criteria. When the rate of change (r) is not given, use the following formulas to compute L:

If L does not come out to a whole number of stations from this formula, it is usually extended to the nearest whole number. Note that this reduces the rate of change. Thus, L = 4.8 stations would be extended to 5 stations, and the value of r computed from r = Δ G/L. These formulas are for road design only. The surveyor must use different formulas for railroad and airfield design.
Station Interval
Once the length of curve is determined, the surveyor selects an appropriate station interval (SI). The first factor to be considered is the terrain. The rougher the terrain, the smaller the station interval. The second consideration is to select an interval which will place a station at the center of the curve with the same number of stations on both sides of the curve. For example, a 300-foot curve could not be staked at 100- foot intervals but could be staked at 10-, 25-, 30-, 50-, or 75-foot intervals. The surveyor often uses the same intervals as those recommended for horizontal curves, that is 10, 25, 50, and 100 feet.
Since the PVI is the only fixed station, the next step is to compute the station value of the PVC, PVT, and all stations on the curve.
PVC = PVI – L/2
PVT = PVI + L/2
Other stations are determined by starting at the PVI, adding the SI, and continuing until the PVT is reached.
Tangent Elevations
Compute tangent elevations PVC, PVT, and all stations along the curve. Since the PVI is the fixed point on the tangents, the surveyor computes the station elevations as follows:
Elev PVC = Elev PVI + (-1 x L/2 x G1)
Elev PVT = Elev PVI + (L/2 x G2)
The surveyor may find the elevation of the stations along the back tangent as follows:
Elev of sta = Elev of PVC + (distance from the PVC x G1).
The elevation of the stations along the forward tangent is found as follows:
Elev of sta = Elev of PVI + (distance from the PVI x G2)

Vertical Maximum
The parabola bisects a line joining the PVI and the midpoint of the chord drawn between the PVC and PVT. In figure 19, line VE = DE and is referred to as the vertical maximum (Vm). The value of Vm is computed as follows: (L = length in 100-foot stations. In a 600-foot curve, L = 6.)

practice, the surveyor should compute the value of Vm using both formulas, since working both provides a check on the Vm, the elevation of the PVC, and the elevation of the PVT.
Vertical Offset. The value of the vertical offset is the distance between the tangent line and the road grade. This value varies as the square of the distance from the PVC or PVT and is computed using the formula:
Vertical Offset = (Distance)2 x Vm
A parabolic curve presents a mirror image. This means that the second half of the curve is identical to the first half, and the offsets are the same for both sides of the curve.
Station Elevation. Next, the surveyor computes the elevation of the road grade at each of the stations along the curve. The elevation of the curve at any station is equal to the tangent elevation at that station plus or minus the vertical offset for that station, The sign of the offset depends upon the sign of Vm (plus for a sag curve and minus for a summit curve).
First and Second Differences. As a final step, the surveyor determines the values of the first and second differences. The first differences are the differences in elevation between successive stations along the curve, namely, the elevation of the second station minus the elevation of the first station, the elevation of the third station minus the elevation of the second, and so on. The second differences are the differences between the differences in elevation (the first differences), and they are computed in the same sequence as the first differences.
The surveyor must take great care to observe and record the algebraic sign of both the first and second differences. The second differences provide a check on the rate of change per station along the curve and a check on the computations. The second differences should all be equal. However, they may vary by one or two in the last decimal place due to rounding off in the computations. When this happens, they should form a pattern. If they vary too much and/or do not form a pattern, the surveyor has made an error in the computation.

Example: A vertical curve connects grade lines G1 and G2 (figure 19). The maximum allowable slope (r) is 2.5 percent. Grades G1 and G2 are found to be -10 and +5.

The vertical offsets for each station are computed as in figure 20. The first and second differences are determined as a check. Figure 21 illustrates the solution of a summit curve with offsets for 50-foot intervals.
High and Low Points
The surveyor uses the high or low point of a vertical curve to determine the direction and amount of runoff, in the case of summit curves, and to locate the low point for drainage.
When the tangent grades are equal, the high or low point will be at the center of the curve. When the tangent grades are both plus, the low point is at the PVC and the high point at the PVT. When both tangent grades are minus, the high point is at the PVC and the low point at the PVT. When unequal plus and minus tangent grades are encountered, the high or low point will fall on the side of the curve that has the flatter gradient.
Horizontal Distance. The surveyor determines the distance (x, expressed in stations) between the PVC or PVT and the high or low point by the following formula:

G is the flatter of the two gradients and L is the number of curve stations.
Vertical Distance. The surveyor computes the difference in elevation (y) between the PVC or PVT and the high or low point by the formula

Example: From the curve in figure 21, G1= + 3.2%, G2 = – 1.6% L = 4 (400). Since G2 is the flatter gradient, the high point will fall between the PVI and the PVT.



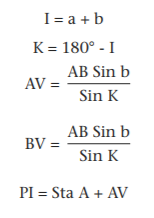
 Reverse Curve Data
Reverse Curve Data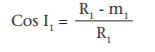

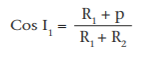 Knowing Cos I1, determine Sin I1.
Knowing Cos I1, determine Sin I1.