Introduction
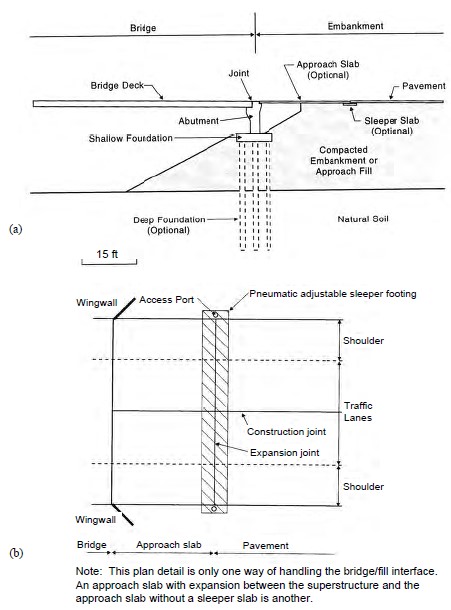
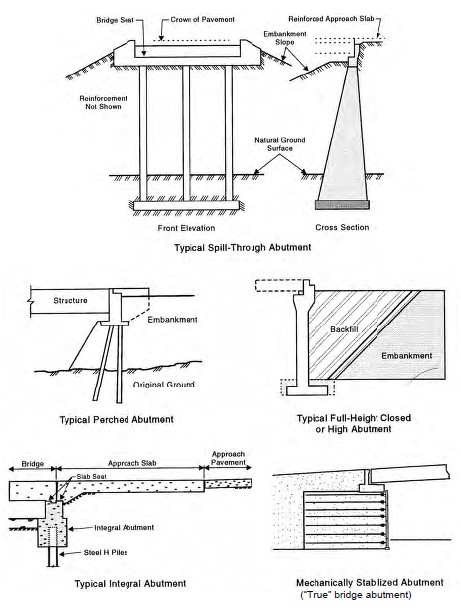
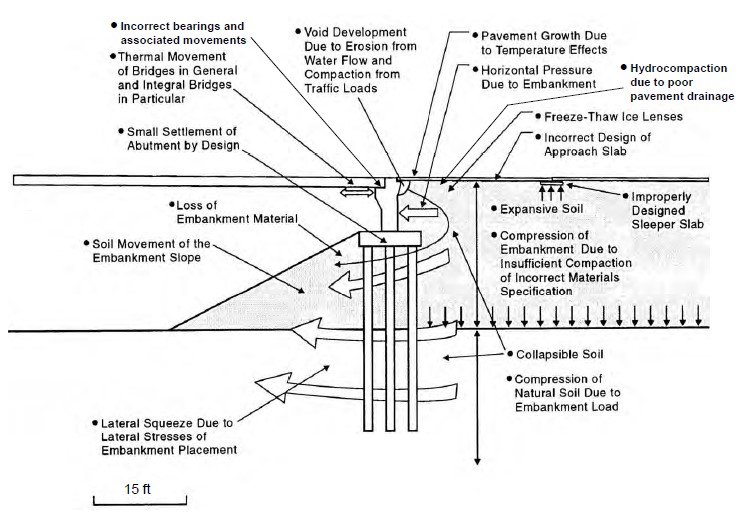
Often roadways are constructed on embankment fills to meet the requirements of the vertical grade of a roadway alignment. Fills placed to accommodate the vertical profile as the roadway approaches a bridge are often referred to as “approach embankment fills” or “approach roadway fills.” Typical elements of a bridge approach system are shown in Figure 1-1. The abutment configuration may vary as shown in Figure 1-2. An abutment fill slope is also referred to as an “end-slope.” The common element to all types of abutments is an approach fill. Deformation, both vertical and lateral, of approach fills is the most prevalent foundation problem in highway construction. The embankment deformation near a bridge structure, leads to the ubiquitous “bump at the end of the bridge.” Figure 1-3 shows some of the problems leading to the existence of the bump.
Approach slabs are often used by most state agencies to provide a smooth transition between the bridge deck and the roadway pavement. The slab usually is designed to withstand some embankment settlement and a reduction in subgrade support near the abutment. Joints must be provided to accommodate cyclic thermal movements of the bridge deck, abutment and roadway pavement. Figure 1-1b shows one common joint set. However, if the approach embankments are not properly engineered, the approach slab merely moves the bump at the end of the bridge to the approach slab-roadway interface. Unlike stability problems, the results of approach embankment deformations are seldom catastrophic but the cost of perpetual maintenance of continuing deformation can be immense. The difficulty in preventing these problems is not so much a lack of technical knowledge as a lack of communication between personnel involved in the roadway design and those involved in the structural design and construction.
1.1 Typical Approach Roadway Deformation Problems
Roadway designers allow use of inexpensive available soils for approach fills to reduce project costs. The bridge structures are necessarily designed for little or no deformation to maintain specified highway clearances and to insure integrity of structural members. In most agencies the responsibility for approach embankment design is not defined as a structural issue, which results in roadway embankment requirements being used up to the structure. In reality, the approach embankment requires special materials and placement criteria to prevent internal deformations and to mitigate external deformations. A discussion of the types of deformation associated with approach fills follows.
Most state agencies, as noted earlier, use bridge approach slabs to provide a transitional roadway between the pavement on the approach embankment and the actual structure of the bridge. Due to the deformation of the approach embankment fills for various reasons shown in Figure 1-3, these slabs can settle and/or rotate creating problems for the abutment as well as the joints. Depending on the configuration of the approach slab, e.g., how the slab is connected to the abutment and/or the wing walls, voids may develop under the slab as the approach fill settles. Such voids can then fill with water, which can further compound the problem, e.g., water pressures acting against structural elements, softening of the soils with associated reduction in strength, freeze-thaw issues, etc. Due to the above considerations, design problems with approach roadway embankments are classified as follows:
- Internal deformation within the embankment
- External deformation in native soils below the embankment
As mentioned previously, it is important to realize that the deformation considerations for the embankment include both vertical as well as lateral deformations. Vertical deformations are commonly referred to as “settlements.” Lateral deformations can result in rotation of the structure that is commonly referred to as “tilting.”
Internal deformation is a direct result of compression of the materials used in the construction of the embankment fill. The importance of adequate drainage with respect to the internal behavior of the embankment cannot be overemphasized. Poor drainage can (a) cause softening of the embankment soils leading to vertical and lateral deformations, (b) reduce the stability of soils near the slope leading to lateral deformations and associated vertical deformations near the crest of the slope, and (c) potentially lead to migration of fill material and creation of voids or substantial vertical and lateral deformations.
External deformation is due to the vertical and lateral deformation of the foundation soils on which the embankment is placed. Furthermore, deformation of foundation soils may include both immediate and consolidation deformations depending on the type of foundation soils. Lateral squeeze of the foundation soils can occur if the soils are soft and if their thickness is less than the width of the end slope of the embankment. Consolidation settlement and lateral squeeze are not an issue within embankment fills since coarse-grained soils placed under controlled compaction conditions are generally used.
This course discusses internal as well as external deformations of approach fills. Design solutions to mitigate the detrimental effect of these deformations are presented. Guidelines for construction monitoring are also provided.
1.2 Internal Deformation Within Embankments
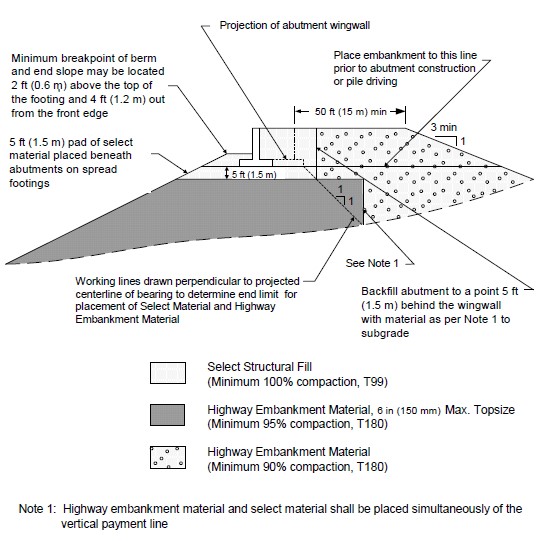
Internal deformation within embankments can be easily controlled by using fill materials that have the ability to resist the anticipated loads imposed on them. A well constructed soil embankment will not excessively deform internally if quality control is exercised with regard to material and compaction. Standard specifications and construction drawings should be prepared for the approach embankment area, normally designated to extend 50 ft (15 m) behind the wingwall. The structural designer should have the responsibility for selecting the appropriate cross section for the approach embankment depending on selection of the foundation type. A typical approach embankment cross section is shown in Figure 1-4.
Special attention should be given to the interface area between the structure and the approach embankment, as this is where the “bump at the end of the bridge” occurs. The reasons for the bump are (a) poor compaction of embankment material near the structure, (b) migration of fine soil into drainage material, and (c) loss of embankment material due to poor drainage details as discussed earlier. Poor compaction is usually caused by restricted access of standard compaction equipment. Proper compaction can be achieved by optimizing the soil gradation in the interface area to permit compaction to maximum density with minimum effort. Figure 1-5 shows a detail for placement of drainage material. Considerations for the specification of select structural backfill and underdrain filter material to minimize the “bump” problem are included in the next two sections. Similar drainage results can be obtained by the use of prefabricated geocomposite drains that are attached to the backwall and connected to an underdrain.
1.2.1 General Considerations for Select Structural Backfill
Select structural backfill is usually placed in relatively small quantities and in relatively confined areas. Structural backfill specifications must be designed to ensure construction of a durable, dense backfill. Table 1-1 lists considerations for the specification of select structural backfill.
1.2.2 General Considerations for Drainage Aggregate
The drainage aggregate, such as that used for underdrain filters, should consist of crushed stone, sand, gravel or screened gravel. Suggested gradation for drainage aggregate is provided in Table 1-2. The AASHTO standard gradation No. 57 or 67 should be equally suitable.
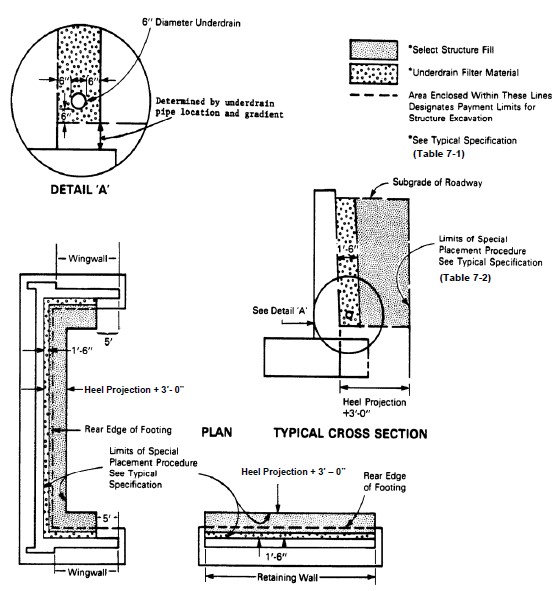


As with the select backfill, the soundness of the drainage aggregate should be tested. The drainage aggregate should have a loss not exceeding 20 percent by weight after four (4) cycles of the magnesium sulfate soundness test.
The maximum loose lift thickness for the drainage aggregate should not exceed 6 in (150 mm). Placement and compaction operations should be conducted in a manner so as to insure that the top surface of each lift of the drainage aggregate should not be contaminated by the adjacent backfill materials. Compaction of the drainage aggregate is commonly achieved by two passes of a vibratory compactor approved by the engineer. No compaction control tests are normally required for the drainage aggregate.
1.2.3 Use of Geosynthetics to Control Internal Deformations
In geographic areas where select materials are not available, the use of geosynthetic materials to reinforce the abutment backfill and approach area can reduce the bump at the end of the bridge. Such reinforced fills can be designed by using the principles of Reinforced Soil Slopes (RSS).
It is suspected that high dynamic loads are routinely induced in the abutment backfill due to vehicle impact loads. Poorly designed or constructed drainage layers or non-durable drainage aggregate can cause either piping of fines or accelerated pavement subsidence due to breakdown of aggregates. As indicated previously, the use of geotextiles or geocomposite drains can be an effective method of minimizing internal embankment deformation and the resulting “bump at the end of the bridge.”
1.3 External Deformation in Foundation Soils Below Embankments
Once the issue of internal deformation within fills has been addressed, the designer must concentrate on the evaluation of the deformation of foundation soils and any engineered soils on which the fills will be placed. Deformations in foundation soils under embankments occur due to the pressure imposed by the embankments. Depending on the type of foundation soils, one or both of the following deformations may occur:
- Immediate (elastic) deformation
- Consolidation (or long-term) deformation
Immediate or elastic deformations occur in all soils regardless of whether they are cohesive or cohesionless. Consolidation deformations typically occur in fine-grained soils that are saturated at the time additional loads are applied. Many and varied procedures exist for computation of these types of deformations. Two methods are presented in this course; one each for cohesionless and cohesive soils. However, there is a critical first step that is common to both modes of deformation. This first step involves the estimation of the stress distribution within the foundation soils due to the pressures imposed by the embankment fills. This step is discussed next.
1.3.1 Procedure for Estimating Stress Distribution in Foundation Soils under Fills
The basic steps involved in estimating stresses in native soils under fills are as follows:
- Develop a soil profile including soil unit weights, SPT results (N160), moisture contents and interpreted consolidation test values.
- Draw effective overburden pressure (po) diagram with depth.
- Plot total embankment pressure (pf) on the po diagram at ground surface level.
- Distribute the total embankment pressure with depth by using the appropriate pressure coefficient charts presented in Figure 1-6.
(Note: The charts in Figure 1-6 are limited to only two locations, Section B-B and Section C-C, and assume that the end and side slopes have the same grades. Programs such as FoSSA (2003) may be used for case of unequal end and side slopes, or if pressure coefficients at locations other than along Section B-B or C-C are desired.)
The principles to remember are: (1) stresses induced in the soil from an embankment load are distributed with depth in proportion to the embankment width, and (2) the additional stresses in the soil decrease with depth.
Following is a step-by-step procedure to use the chart in Figure 1-6. A worked example is presented afterwards to illustrate the use of the chart numerically:
Step 1. Determine the distance bf from the centerline of the approach embankment to the midpoint of side slope. Multiply the numerical value of “bf” by the appropriate values shown to the right of the chart to develop the depths at which the distributed pressures will be computed, e.g., 0.2bf, 0.4bf, etc.
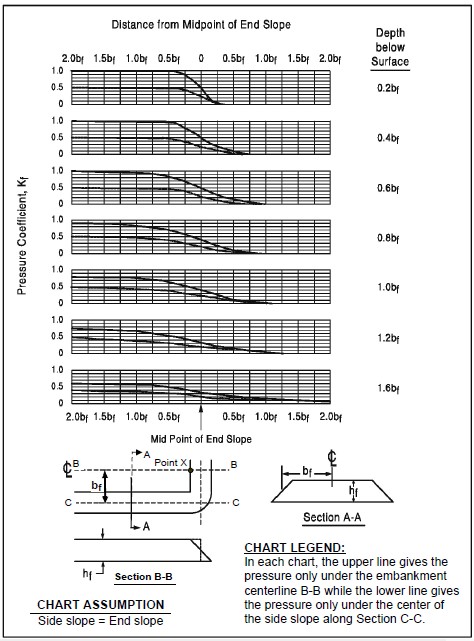
Step 2. Select the point X on the approach embankment where the vertical stress prediction is desired, normally at the intersection of the centerline of the embankment and the abutment. In this case the side slope is called the end slope. Measure the distance from X to the midpoint of the end slope. Return to the chart and scale that distance as a multiple of bf on the horizontal axis from the appropriate side of the midpoint centerline line of the end slope.
Step 3. Read vertically up or down from the plotted distance on the horizontal axes to the various curves corresponding to depth below surface. The “Kf” value on the left vertical axis should be read and recorded on a computation sheet with the corresponding depth. Note that the upper line gives the pressure under the embankment centerline (Section B-B) while the lower line gives the pressure under the mid of the side slope (Section C-C).
Step 4. Multiply each “Kf” value by the value of total embankment pressure (γfhf) to determine the amount of the pressure increment (∆p) transmitted to each depth, where γf is the unit weight of the embankment fill soil and hf is height of the embankment fill.
The application of this step-by-step procedure and the charts shown on Figure 1-6 to a typical embankment problem is illustrated by the following worked example problem.
Example 1-1: The geometry of a fill slope is as follows:
Fill height hf = 30 ft; Fill unit weight γf = 100 pcf
End and side slopes (2H:1V); Embankment top width = 100 ft

Find: The stress increase (∆p) under the proposed abutment centroid (Point X) at a depth of 0.8 bf below the base of the fill.
Solution:
Figure 1-6 will be used to determine the stress increase. To use the chart first compute the following quantities:
- Distance from midpoint of end slope to Point X = 30 ft.
- Distance from centerline to mid point of side slope bf = (100 ft/2) + (60 ft/2) = 80 ft.
Enter stress distribution chart for a depth of 0.8bf = (0.8)(80 ft) = 64 ft and a distance measured from the midpoint of the end slope to Point X expressed as a multiple of bf = (30 ft/80 ft) bf = 0.38 bf. Enter the plot with this value to the left of the value of zero on the abscissa, i.e., upslope from the midpoint on the end slope.
In Figure 1-6 read Kf = 0.7 from the chart for 0.8bf. Therefore, at a depth of 64 ft below the embankment at Point X

Repeat the above steps for distances to other points along the centerline of the embankment expressed as a multiple of bf and measured (+ and -) from the midpoint of end slope to develop the horizontal distribution of vertical stress increases due to the embankment at a depth of 64 ft below and beyond the base of the end slope along the embankment centerline.
Horizontal Distribution of Vertical Stress Increases Below and Beyond the End Slope at a Depth of 64-ft Below the Embankment

1.4 Computation of Immediate Settlement
All geomaterials, whether cohesionless or cohesive, will experience settlements immediately after application of loads. Whether or not the settlements will continue with time after the application of the loads will be a function of how quickly the water can drain from the voids. Long-term consolidation-type settlements are generally not experienced in cohesionless soils where pore water can drain quickly or in dry or slightly moist cohesive soils where significant amounts of pore water are not present. Therefore, embankment settlements caused by consolidation of cohesionless or dry cohesive soil deposits are frequently ignored as they are much smaller compared to immediate settlements in such soils. Consolidation type settlement for saturated cohesive soils is discussed in Section 1.5.
Many methods have been published in the geotechnical literature for the computation of immediate settlements in soils or rocks. These methods vary from the use of rules of thumb based on experience to the use of complex nonlinear elasto-plastic constitutive models. All methods are based on some form of estimate of soil compressibility. In the geotechnical literature, soil compressibility is expressed using several different terms such as “bearing capacity index,” “compression index,” “elastic modulus,” “constrained modulus,” etc.
For computing external embankment settlements, the method by Hough (1959) as modified by AASHTO (2004 with 2006 Interims) can be used since it is simple and provides a first-order conservative estimate of immediate settlements. The original Hough method (Hough, 1959) was based on uncorrected SPT N-values and included recommendations for cohesionless as well as cohesive soils such as sandy clay and remolded clay. AASHTO modified the Hough (1959) method for use with N160 values and eliminated the recommendations for sandy clay and remolded clay. Since the method presented here is AASHTO’s version of the Hough method, it will be referred to as the “Modified Hough” method.
Even after the modifications, the settlements estimated by Modified Hough method are usually overestimated by a factor of 2 or more based on the data in FHWA (1987). While such conservative estimates may be acceptable from the viewpoint of the earthwork quantities (see discussion regarding compaction factor in Section 1.4.1.1), they may be excessive with respect to the behavior of the structures founded within, under or near the embankment. In cases where structures are affected by embankment settlement, more refined estimates of the immediate settlements are warranted. For more refined estimates of immediate settlements it is recommended that the designer use either the modified method of Schmertmann, et al. (1978), which takes into account the strain distribution with depth, or the D’Appolonia (1968, 1970) method, which takes into account the effect of preconsolidation. Both methods provide equally suitable results.
1.4.1 Modified Hough Method for Estimating Immediate Settlements of Embankments
The following steps are used in Modified Hough method to estimate immediate settlement:
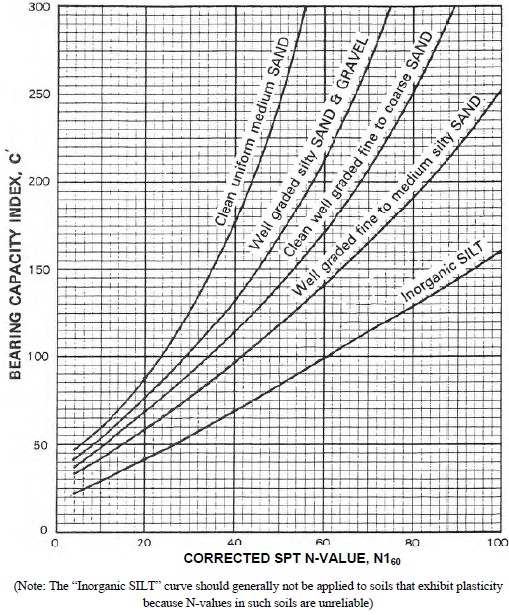
Step 1. Determine the bearing capacity index (C′) by entering Figure 1-7 with N160 value and the visual description of the soil.
Step 2. Compute settlement by using the following equation. Subdivide the total thickness of the layer impacted by the applied loads into 10 ft ± (3 m ±) increments and sum the incremental solutions:
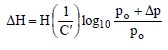
where:
- ΔH = settlement of subdivided layer (ft)
- H = thickness of subdivided soil layer considered (ft)
- C′ = bearing capacity index (Figure 1-7)
- po = existing effective overburden pressure (psf) at center of the subdivided layer being considered. For shallow surface deposits, a minimum value of 200 psf should be used to prevent unrealistic settlement predictions.
- Δp = distributed embankment pressure (psf) at center of the subdivided layer being considered
Note that the term po + ∆p represents the final pressure applied to the foundation subsoil, pf.
A key point is that the logarithm term in Equation 1-1 incorporates the fundamental feature of dissipation of applied stress with depth. The use of Modified Hough method is illustrated numerically in Example 1-2.
Example 1-2: For the geometry shown in the following figure, determine the settlement at the center of a wide embankment placed on a silty sand layer by using Modified Hough method and the po diagram.

Solution:
The original overburden pressure at the center of the 10 ft thick silty sand deposit can be computed as po = (10 ft/2) (120 pcf) = 600 psf. Since, the embankment is “wide” the stress does not practically dissipate with depth. Therefore, increase in the stress at this depth due to the 20 ft high wide embankment can be computed as ∆p = (20 ft) (120 pcf) = 2,400 psf. The po diagram based on these values of po and ∆p is shown below.

From Figure 1-7, find C′ for “silty sand.” Using N160 = 20 and the “silty sand” curve, C′ ≈ 58. Find immediate settlement using Equation 1-1 as follows:

1.4.1.1 Comments on the Computed Settlement of Embankments
The implication of the amount of embankment settlement is that when the embankment is completed, additional fill will be required to bring the top of the embankment to the design grade. For example, a 1 in (25 mm) settlement on a 60-ft (18 m) wide, 1-mile (5,280 ft or 1,610 m) long embankment will result in a need for approximately 1,000 yd3 (~750 m3) of additional fill. Some state agencies refer to such settlement estimates as the “compaction factor” and note it in the contract plans so that the contractor can make appropriate allowances in the bid price to accommodate the additional embankment fill material needed to achieve the required design grades. It is in this regard the conservative estimate of the settlement resulting from the Modified Hough method may be acceptable and may even be preferable to prevent construction change orders.
1.5 Computation of Consolidation (Long-Term) Settlements
Unless the geomaterial is friable, consolidation settlements in fine-grained saturated soils occur over a period of time as a function of the permeability of the soils. In this course the data obtained from the consolidation test are used to demonstrate the computation of long-term settlements due to the consolidation phenomena, i.e., primary consolidation and secondary compression.
Theoretically, a necessary condition for consolidation settlement is that the soil must be saturated, i.e., degree of saturation, S = 100%. While the laboratory test for moisture content of a soil is inexpensive and relatively straightforward to perform and generally yields reliable, reproducible results, there are a number of parameters in consolidation analysis that cannot be determined with confidence. Therefore, depending on the magnitude and configuration of the load with respect to the size and moisture content of the compressible soil layer, it is possible that consolidation settlements may occur in soils that are judged to be “nearly saturated” but not “fully saturated.” This is because such nearly saturated soils may approach full saturation after application of a load of sufficient magnitude to cause the pore spaces filled with air to compress (immediate settlement) to the extent that the degree of saturation is virtually 100%. Therefore, the geotechnical specialist should carefully evaluate the in-situ degree of saturation with respect to the degree of saturation of the soil sample at the beginning and end of the consolidation test. The geotechnical specialist should also carefully evaluate the reliability of other parameters determined during the performance of the consolidation test to make an informed judgment regarding the potential for consolidation settlements to occur. Unnecessarily conservative assumptions regarding the magnitude and time rate of consolidation settlements may lead to recommendations for deep foundations or for unnecessary implementation of costly ground improvement measures.
Settlement resulting from primary consolidation may take months or even years to be completed. Furthermore, because soil properties may vary beneath the location of loading, the duration of the primary consolidation and the amount of settlement may also vary with the location of the applied load, resulting in differential settlement. If such settlements are not within tolerable limits the geotechnical feature as well as a structure founded on or in it may be damaged. In the case of embankments, differential settlements that occur along the longitudinal axis of the embankment because of changes in thickness and/or consolidation properties of underlying clays can cause transverse cracking on the surface of the embankment where pavement structures are usually constructed.
When the areal extent of the applied load is wide compared to the thickness of the compressible layer beneath it, a large portion of the soil will consolidate vertically (onedimensionally) with very little lateral displacement because of the constraining forces exerted by the neighboring soil elements. However, when the areal extent of the applied load is smaller than the thickness of the compressible layer or when there is a finite soft layer at a certain depth below the loaded area, significant lateral stresses and associated deformations can occur. Back-to-back retaining walls and a narrow embankment for an approach ramp on soft soils are examples of this condition. Due to the potential for significant lateral stresses and associated lateral deformations, the geotechnical specialist should carefully evaluate the loading geometry with respect to subsurface conditions and ascertain whether the problem is 1-D or 3-D. This type of evaluation is important because 3-D deformations can affect a number of facilities such as buried utilities, bridge foundations, and the stability of embankment slopes.
The determination of the vertical component of 3-D consolidation deformation is commonly based on the one-dimensional consolidation test (ASTM D 2435). Typically, the results of the one-dimensional consolidation test are expressed in an e-log p plot which is the so-called “consolidation curve.” Settlement due to consolidation can be estimated from the slope of the consolidation curve. This procedure is generally used in practice despite the fact that not all of the points beneath the embankment undergo one-dimensional consolidation. However, before the laboratory test results are used, it is very important to correct the consolidation curves for the effects of sampling. Thus, before proceeding with the discussion of computing consolidation settlements, the correction of the laboratory consolidation curves is discussed.
1.5.1 Correction of Laboratory One-Dimensional Consolidation Curves
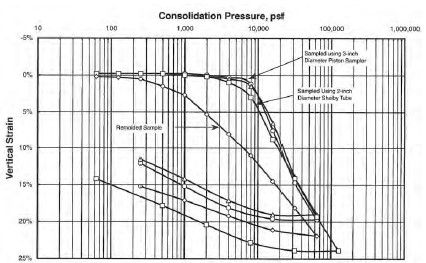
The process of sampling soils will cause some disturbance no matter how carefully the samples are taken. This sampling disturbance will affect virtually all measured physical properties of the soil. The sampling disturbance will usually cause the “break” in the laboratory consolidation curve to occur at a lower maximum past vertical pressure (pc) than would be measured for a truly undisturbed specimen. The effect of disturbance from the sampling procedure is illustrated in Figure 1-8 where, for the sake of comparison, the vertical strain rather than void ratio (e) is plotted versus the logarithm of the vertical effective stress.
Figure 1-8 shows three consolidation curves for a red-colored plastic clay from Fond du Lac, Wisconsin. Samples were taken alternately with 3 in (75 mm) and 2 in (50 mm) thin walled samplers. The 3 in (50 mm) sampler apparently caused less disturbance than the 2 in (50 mm) sampler. The curve for the remolded sample is the flattest curve without a well defined break between reloading and virgin compression.
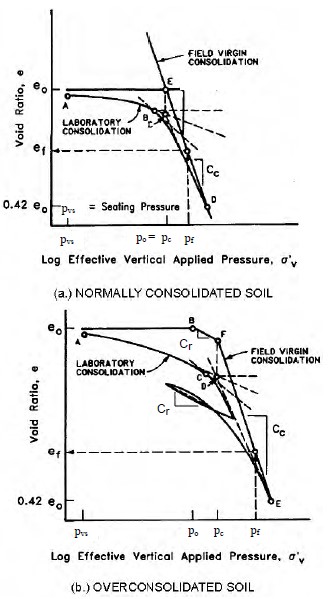
Even for good quality samples, it is still necessary to “correct” the e-log p curve since no sampling technique is perfect. There are several methods available to correct the consolidation curve. The laboratory curve can be corrected according to Figures 1-9a and 19b for normally consolidated and overconsolidated soils, respectively. Table 1-3 presents the reconstruction procedures.

1.5.2 Computation of Primary Consolidation Settlements
Depending upon the magnitude of the existing effective stress relative to the maximum past effective stress at a given depth, in-situ soils can be considered normally consolidated, overconsolidated (preconsolidated), or underconsolidated. The behavior of in-situ soils to additional loads is highly dependent upon the stress history. The overconsolidation ratio, OCR, which is a measure of the degree of overconsolidation in a soil is defined as pc/po. The value of OCR provides a basis for determining the effective stress history of the clay at the time of the proposed loading as follows:
- OCR = 1 – the clay is considered to be “normally consolidated” under the existing load,
i. e., the clay has fully consolidated under the existing load (pc = po). - OCR > 1 – the clay is considered to be “overconsolidated” under the existing load, i.e., the clay has consolidated under a load greater than the load that currently exists (pc > po).
- OCR < 1 – the clay is considered to be “underconsolidated” under the existing load, i.e., consolidation under the existing load is still occurring and will continue to occur under that load until primary consolidation is complete, even if no additional load is applied (pc < po).
The manner in which primary settlements are computed for each of these three conditions varies as will be discussed in the following sections.
1.5.2.1 Normally Consolidated Soils
The settlement of a geotechnical feature or a structure resting on n layers of normally consolidated soils (pc = po) can be computed from Figure 1-10a where n is the number of layers into which the consolidating layer is divided:
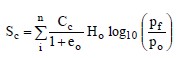
where:
- Cc = compression index
- eo = initial void ratio
- Ho = layer thickness
- po = initial effective vertical stress at the center of layer n
- pf = po+ Δp = final effective vertical stress at the center of layer n.
The final effective vertical stress is computed by adding the stress change due to the applied load to the initial vertical effective stress. The total settlement will be the sum of the compressions of the n layers of soil.
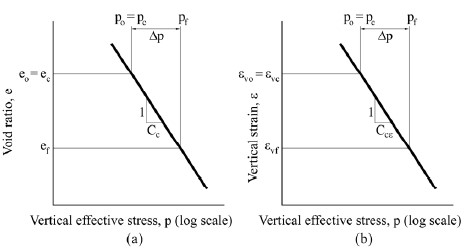
Normally the slope of the virgin portion of the e-log p curve is determined from the corrected one-dimensional consolidation curve measured on specimens taken from each relevant soil in the stratigraphic profile. The procedure for determining the corrected curve is presented in Table 1-6a.
Sometimes the consolidation data is presented in terms of vertical strain (εv) instead of void ratio. In this case the slope of the virgin portion of the modified consolidation curve is called the modified compression index and is denoted as Ccε as shown in Figure 1-10b. Settlement is computed by using Equation 1-3 for normally consolidated soils where all of the other terms are defined as for Equation 1-2.
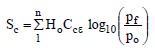
By comparing Equations 7-2 and 7-3, it can be seen that Ccε = Cc / (1+eo)
1.5.2.2 Overconsolidated (Preconsolidated) Soils
If the water content of a clay layer below the water table is closer to the plastic limit than the liquid limit, the soil is likely overconsolidated, i.e., OCR >1. This means that in the past the clay was subjected to a greater stress than now exists. Preconsolidation could have occurred because of any number of factors including but not limited to the weight of glaciers which is especially prevalent in the northern tier of states and in the northeast, the weight of a natural soil deposit that has since eroded away, the weight of a previously placed fill that has since been removed, loads due to structures that have since been demolished, desiccation, etc.
As a result of preconsolidation, the field state of stress will reside on the initially flat portion of the e-log p curve. Figures 1-11a and 1-11b illustrate the case where a load increment, ∆p, is added so that the final stress, pf, is greater than the maximum past effective stress, pc. For this condition, the settlements for the case of n layers of overconsolidated soils will be computed from Equation 1-4 or Equation 1-5 that correspond to Figure 1-11a and 1-11b, respectively.
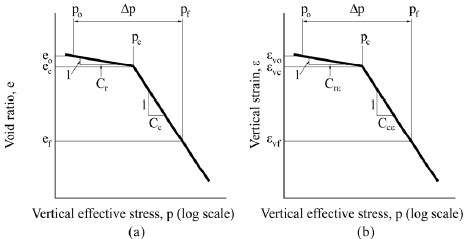
The total settlement is computed by summing the settlements computed from each subdivided compressible layer within the zone of influence (ZI). The assumption is made that the initial and final stress calculated at the center of each sublayer is representative of the average stress for the sublayer, and the material properties are reasonably constant within the sublayer. The sublayers are typically 5 ft (1.5 m) to 10 ft (3 m) thick in highway applications. In cases where the various stratigraphic layers represent combinations of both normally and overconsolidated soils, the settlement is computed by using the appropriate combinations of Equations 1-2 through 1-5.
1.5.2.3 Underconsolidated Soils
Underconsolidation is the term used to describe the effective stress state of a soil that has not fully consolidated under an existing load, i.e., OCR < 1. Consolidation settlement due to the existing load will continue to occur under that load until primary consolidation is complete, even if no additional load is applied. This condition is shown in Figure 1-12 by ∆po. Therefore, any additional load increment, ∆p, would have to be added to po. Consequently, if the soil is not recognized as being underconsolidated, the actual total primary settlement due to ∆po+∆p will be greater than the primary settlement computed for an additional load ∆p only, i.e., the settlement may be under-predicted. As a result of under-consolidation, the field state of stress will reside entirely on the virgin portion of the consolidation curve as shown in Figure 1-12. The settlements for the case of n layers of under-consolidated soils are computed by Equation 1-6 or Equation 1-7 that correspond to Figure 1-12a and 1-12b, respectively.
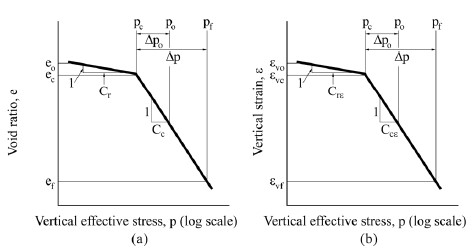
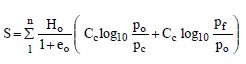
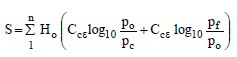
1.5.3 Consolidation Rates (Time Rate of Consolidation Settlement)
The rate of consolidation should be considered for the design of geotechnical features and structures on compressible clay. For example, a geotechnical feature such as an embankment will settle relative to a bridge foundation supported on piles, creating an undesirable “bump at the end of the bridge.” Hence, time rate of consolidation, as well as differential settlements between the bridge and embankment, is important. The concept of time rate of consolidation is explained with respect to Figure 1-13.
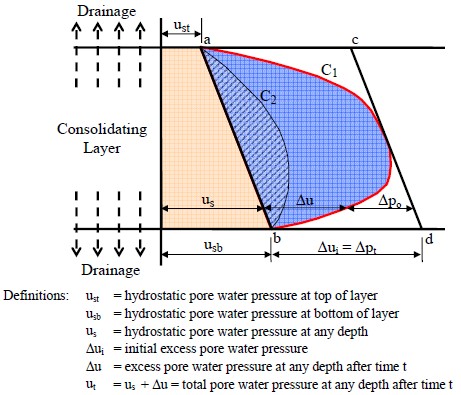
- The initial hydrostatic pore water pressure distribution, us, is assumed to be linear in a layer of saturated clay. Line a-b in Figure 1-13 shows the initial hydrostatic pore water pressure distribution through a clay layer at a certain depth below the ground water elevation where ust is the pore water pressure at the top of the clay layer and usb is the pore water pressure at the bottom of the clay layer. Experimental measurement of pore pressures in saturated clays subjected to one-dimensional loading indicate that when a load is applied the pore water pressure will instantaneously increase an amount equal to the total vertical stress increment, ∆pt, uniformly throughout the entire thickness of the consolidating layer as shown by a-c-d-b in Figure 1-13. The initial increase in the pore water pressure, ∆ui, above the static value is called the initial excess pore water pressure and it is equal to ∆pt. The total initial pore water pressure which is the sum of the hydrostatic pressure and the initial excess pore water pressures is shown as line c-d in Figure 1-13.
- With time, water will drain out of the consolidating layer to relieve the excess pore water pressure and the applied total vertical stress increment, ∆pt, will be slowly transferred to the soil particles, i.e., at any given time after application of the load, the initial excess pore water pressure will decrease at all depths to an excess pore water pressure having a value less than of ∆ui. The pattern of the excess pore water pressure at any given time is not parallel to line c-d, but is curvilinear similar to curve C1 in Figure 1-13. Curves such as C1 and C2 are known as iscochrones because they are lines of equal time. The difference between the line a-b and curve C1, for example, represents the excess pore water pressure, ∆u, at any point within the consolidating layer at any time after application of the vertical load stress increment, ∆pt.
- If the clay layer is confined between two sand layers that are more permeable, the initial excess pore water pressure will drop immediately to zero at the drainage boundaries as shown in Figure 1-13 and the total vertical stress increment ∆pt and will be equal to the effective vertical stress increment, ∆po. The rate of this transfer with depth depends upon the boundary drainage conditions. With time, the vertical distribution of excess pore water pressure within the consolidating layer will evolve from the initial distribution (a c-d-b), to the C1 distribution, to the C2 distribution, and finally to the initial distribution of the hydrostatic pressure represented by line a-b.
- At any depth, the difference between a pore water pressure isochrone, such as C1, and the initial excess pore water pressure c-d is equal to the effective vertical stress increment, ∆po, i.e., the amount of ∆pt that has been transferred to the soil structure. Since the isochrone C1 develops after a certain period of time, the difference between C1 and c-d also represents the distribution of the effective stress increments with depth at a given time after application of load.
- Note that the distribution shown in Figure 1-13 pertains only to the specific boundary drainage condition where a more permeable material exists above and below the consolidating clay layer. In this case the clay layer is considered to be “doubly drained” with the longest distance to a drainage boundary being half the layer thickness. If the clay layer is underlain by a less permeably material (e.g., rock), drainage will occur in only one direction and the isochrones at a given time will be different from those shown for double drainage in Figure 1-13. In this case the clay layer is considered to be “singly drained” with the longest distance to a drainage boundary being the entire layer thickness. During the consolidation process the principle of effective stress will be in operation at every depth, i.e., ∆pt = ∆u + ∆po and settlement will be occurring due to the effective stress increment ∆po. The drainage boundary condition will affect the time it takes for settlement to occur, but it has no effect on the magnitude of settlement, which is determined by use of the equations presented previously in which settlement is a function of ∆po only.
1.5.3.1 Percent Consolidation
As indicated previously, immediately after application of load, ∆u, will drop to zero at the drainage boundaries because the water will drain immediately into the more pervious layers. Since the excess pore water pressure is zero at the drainage boundaries, the soil there has undergone 100% consolidation. However, at interior points, the pore water pressure dissipates more slowly with time depending on the permeability of the compressible soil. At any time after application of a load, the actual degree or percentage of consolidation at a given depth is defined as (∆ui-∆u)/∆ui, where ∆u is the excess pore water pressure at that depth at that time and ∆ui = the initial excess pore water pressure which, as indicated previously, equals the total stress increment ∆pt. Thus, where ∆ui = ∆u (i.e., at the instant of loading), the percent consolidation is zero. When ∆u= 0 (i.e., at the end of consolidation), the percent consolidation is 100. This relationship is valid at any depth within the consolidating layer at any time from the instant of loading to the completion of primary consolidation.
While plots of the type shown in Figure 1-13 give an indication of the pore pressure variation within the consolidating layer at any time and are useful to explain the theory of consolidation, from a practical viewpoint it is usually more beneficial to obtain the average degree or percent of consolidation, U, within the entire layer to indicate when the entire clay layer has undergone a certain average amount of consolidation of say 10, 50, or 80 percent. With reference to Figure 1-13, the average degree of consolidation at any time is defined as the difference between the area under the initial excess pore water pressure curve (a-c-d-b) and the area under the isochrone at that time, e.g., the cross hatched area under isochrone C2 divided by the area under the initial excess pore water pressure curve (a-c-d-b). The result is expressed as a percentage. Therefore, at the instant ∆pt is applied the area under the isochrone is exactly equal to the area (a-c-d-b) as indicated above and the average percent consolidation (U) equals zero. At the end of primary consolidation all excess pore water pressures have dissipated and the area under the isochrone is zero. Thus, the average percent consolidation (U) equals 100. Since, according to the principle of effective stress, ∆pt = ∆u + ∆po, the amount of settlement at any time after the application of load is directly related to the amount of consolidation that has taken place up to that time. As a practicality the average degree of consolidation at any time, t, can be defined as the ratio of the settlement at that time, St, to the settlement at the end of primary consolidation, Sultimate, when excess pore water pressures are zero throughout the consolidating layer, i.e., U= St/Sultimate. This relationship is used to develop a so-called “settlement-time curve” as will be discussed later.
Table 1-4 shows the average degree of consolidation (U) corresponding to a normalized time expressed in terms of a time factor, Tv, where:
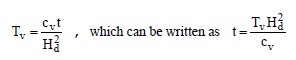
where:
- cv = coefficient of consolidation (ft2/day) (m2/day)
- Hd = the longest distance to a drainage boundary (ft) (m)
- t = time (day).
Any consistent set of units can be used in Equation 1-8 since Tv is dimensionless. As indicated previously, the longest drainage distance of a soil layer confined by more permeable layers on both ends is equal to one-half of the layer thickness. When confined by a more permeable layer on one side and an impermeable boundary on the other side, the longest drainage distance is equal to the layer thickness. The value of the dimensionless time factor Tv may be determined from Table 1-4 for any average degree of consolidation. U. The actual time, t, it takes for this percent of consolidation to occur is a function of the boundary drainage conditions, i.e., the longest distance to a drainage boundary, as indicated by Equation 1-8. By using the normalized time factor, Tv, settlement time can be computed for various percentages of settlement due to primary consolidation, to develop a predicted settlement-time curve. A typical settlement-time curve for a clay deposit under an embankment loading is shown in Figure 1-14.


1.5.3.2 Step-by-Step Procedure to Determine Amount and Time for Consolidation
The step-by-step process for determining the amount of and time for consolidation to occur for a single-stage construction of an embankment on soft ground is outlined below:
- From laboratory consolidation test data determine the e-log p curve and estimate the change in void ratio that results from the added weight of the embankment. Create the virgin field consolidation curve by using the guidelines presented in Table 1-3.
- Determine if the foundation soil is normally consolidated, overconsolidated or under-consolidated.
- Use Equations 1-2 to 1-7 to compute the primary consolidation settlement for normally consolidated, overconsolidated and under-consolidated foundation soils.
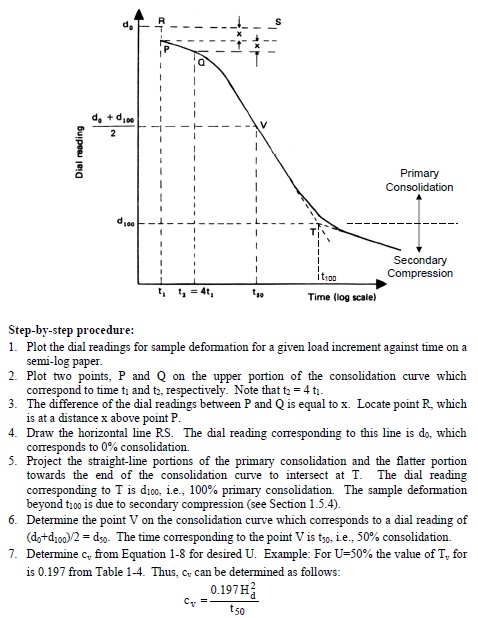
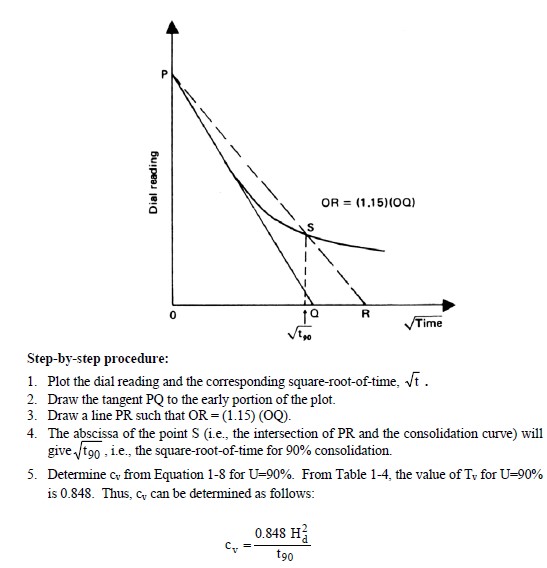
- Determine cv from laboratory consolidation test data. Two graphical procedures are commonly used for this determination are the logarithm-of-time method (log t) proposed by Casagrande and Fadum (1940) and the square-root-of-time method ( t ) proposed by Taylor (1948). These methods are shown in Figures 1-15 and 116, respectively. Because both methods are different approximations of theory, they do not give the same answers. Often the t method gives slightly greater values of cv than the log t method.
- Use Equation 1-8 to calculate the time to achieve 90% – 95% primary consolidation.
For a more detailed discussion on the consolidation theory, the reader is referred to Holtz and Kovacs (1981). An alternative approach to hand calculations is the use of a computerized method. For example, program FoSSA (2003) by ADAMA Engineering, Version 1.0 licensed to FHWA, calculates the time rate of settlement for various boundary conditions including the effects of staged construction and strip drains in addition to calculating the stresses and settlements. FoSSA (2003) also allows for simulation of multiple layers undergoing simultaneous consolidation. In any event, the step by-step hand calculations can serve to verify the correctness of benchmark cases and thereby be used to ascertain the correctness of any computerized procedure.
Comments on cv value: The value of cv is determined for a given load increment. It varies from increment to increment and is different for loading and unloading. Moreover, cv, usually varies considerably among samples of the same soil. Therefore, if the actual rate of consolidation is critical to the design, as in certain stability problems where excess pore water pressures must be known accurately, pore pressures must actually be measured in the field as construction proceeds.
Regardless of whether hand-calculations or computerized methods are used, the important factors to remember are:
- the time required for consolidation is proportional to the square of the longest distance required for water to drain from the deposit and,
- the rate of settlement decreases as time increases.
The maximum length of vertical drainage path, Hd, bears further explanation. This term should not be confused with the H term in the equation for the computation of the settlement magnitude. H is an arbitrarily selected value usually representing a portion of the total compressible layer thickness. For calculating the magnitude of settlement the sum of the sublayer H values must equal the total thickness of the clay layer. For calculating the time rate of settlement, the Hd term in Equation 1-8 is the maximum vertical distance that a water molecule must travel to escape from the compressible layer to a more permeable layer. In the case of a 20 ft (6 m) thick clay layer bounded by a sand layer on top and a virtually impermeable rock stratum on the bottom, the Hv term would equal to 20 ft (6 m). The water molecule must travel from the bottom of the layer to the top of the layer to escape, i.e., single drainage. However, if the clay layer was bounded top and bottom by more permeable sand deposits, the Hv distance would be 10 ft (3 m). The water molecule in this case, needs only to travel from the center of the layer to either boundary to escape, i.e., double drainage. However, regardless of the boundary drainage conditions, the sum of the sublayer H values must equal 20 ft (6 m) in the settlement computations.
The mechanism for determining the maximum horizontal path for escape of a water molecule is similar. The influence of horizontal drainage may be significant if the width of the loaded area is small. For instance, during consolidation under a long, narrow embankment, a water molecule can escape by traveling a distance equal to one half the embankment width. However, for very wide embankments the beneficial effect of lateral drainage may be small as the time for lateral escape of a water molecule increases as the square of one-half the embankment width.
The concepts of consolidation settlement and time rates of consolidation with reference to an embankment loading are illustrated by the following example.
Example 1-3: Determine the magnitude of and the time for 90% consolidation for the primary settlement of a “wide” embankment by using the po diagram.

Solution:
Since the embankment is “wide,” the vertical stress at the base of the embankment is assumed to be the same within the 10-ft thick clay layer. Since soil is normally consolidated, use Equation 1-2 to determine the primary consolidation settlement as follows:

Find time for 90% consolidation use Tv = 0.848 from Table 1-4. Assume single vertical drainage due to impervious rock underlying clay layer and use Equation 7-8 to calculate the time required for 90% consolidation to occur.

1.5.4 Secondary Compression of Cohesive Soils
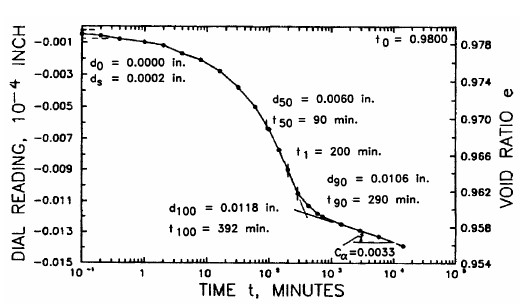
Secondary compression is the process whereby the soil continues to displace vertically after the excess pore water pressures are dissipated to a negligible level i.e., primary compression is essentially completed. Secondary compression is normally evident in the settlement-log time plot when the specimen continues to consolidate beyond 100 percent of primary consolidation, i.e., beyond t100, as shown in Figure 1-15. An example is shown in Figure 1 17, where secondary compression occurs beyond t100 = 392 mins. There are numerous hypotheses as to the reason for the secondary compression. The most obvious reason is associated with the simplifications involved in the theory of one-dimensional consolidation derived by Terzaghi. More rigorous numerical solutions accounting for the simplifications can often predict apparent secondary compression effects.
The magnitude of secondary compression is estimated from the coefficient of secondary compression, Cα, as determined from laboratory tests by using Equation 1-9 that is derived from Figure 1-17.
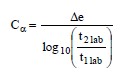
where:
- t1 lab = time when secondary compression begins and is typically taken as the time when 90 percent of primary compression has occurred
- t2 lab = an arbitrary time on the curve at least one log-cycle beyond t90 or the time corresponding to the service life of the structure
The settlement due to secondary compression (Ss) is then determined from Equation 1-10.
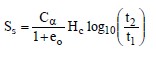
where:
- t1 = time when approximately 90 percent of primary compression has occurred for the actual clay layer being considered as determined from Equation 7-8.
- t2 = the service life of the structure or any other time of interest.
The values of Cα can be determined from the dial reading vs. log time plots associated with the one-dimensional consolidation test as shown in Figure 1-17. Typical ranges of the ratio of Cα/Cc can be used to check laboratory test results.
1.6 Lateral Squeeze of Foundation Soils
When the geometry of the applied load is larger than the thickness of the compressible layer or when there is a finite soft layer within the depth of significant influence (DOSI) below the loaded area, significant lateral stresses and associated lateral deformations can occur. For example, as shown in Figure 1-18, if the thickness of a soft soil layer beneath an embankment fill is such that it less than the width, be, of an end or side slope, then the soft soil may squeeze out.
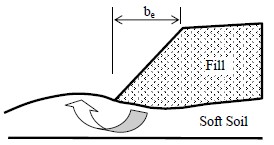
The lateral squeeze phenomenon is due to an unbalanced load at the surface of the soft soil. The lateral squeeze behavior may be of two types, (a) short-term undrained deformation that results from a local bearing capacity type of deformation, or (b) long-term drained, creep-type deformation. Creep refers to the slow deformation of soils under sustained loads over extended periods of time and can occur at stresses well below the shear strength of the soil. Secondary compression is a form of creep deformation while primary consolidation is not.
The lateral squeeze phenomenon can be observed in the field. For example, field observations and measurements have shown that some bridge abutments supported on piles driven through compressible soils tilted toward the embankment fill. Many of the abutments experienced large horizontal movements resulting in damage to the structure. The cause of this problem is attributed to the unbalanced fill load, which “squeezes” the soil laterally as discussed previously. This “lateral squeeze” of the soft foundation soil can apply enough lateral thrust against the piles to bend or even shear the piles. This problem is illustrated in Figure 1-19. The bridge abutment may tilt forward or backward depending on a number of factors including the relative configuration of the fill and the abutment, the relative stiffness of the piles or shafts and the soft deposit, the strength and thickness of the soft layer, rate of construction of the fill, and depth to bearing layer.
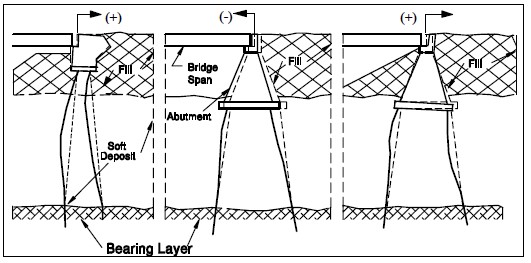
1.6.1 Threshold Condition for Lateral Squeeze
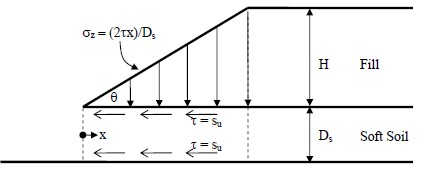
Experience has shown that lateral squeeze of the foundation soil can occur and abutment tilting may result if the surface load applied by the weight of the fill exceeds 3 times the undrained shear strength, su, of the soft foundation soil, i.e.,
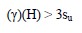
where, γ is the unit weigh of the fill and H is the height of the fill. The possibility of abutment tilting can be evaluated in design by using the above relationship. Whether the lateral squeeze will be short-term or long-term can be determined by evaluating the consolidation rate of settlement with respect to the rate of application of the load. For practical purposes, the unit weight of an embankment fill can be assumed to be approximately 125 pcf (19.7 kN/m3). The undrained shear strength, su, of the foundation soil can be determined either from in-situ field vane shear tests or from laboratory triaxial tests on high quality undisturbed Shelby tube samples.
1.6.2 Calculation of the Safety Factor against Lateral Squeeze
The safety factor against failure by squeezing, FSSQ, may be calculated by Equation 1-12 (Silvestri, 1983). The geometry of the problem and the forces involved are shown in Figure 1-20.
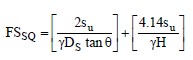
where:
- θ = angle of slope
- γ = unit weight of the fill
- DS = depth of soft soil beneath the toe of the end slope or side slope of the fill
- H = height of the fill
- su = undrained shear strength of soft soil beneath the fill
Caution is advised when Equation 1-12 is used. It was found that when FSSQ < 2, a rigorous slope stability analysis and possibly advanced numerical analysis, e.g., finite element analysis should be performed. When the depth of the soft layer, DS, is greater than the base width of the end slope, b=H/tanθ, general slope stability behavior governs the design. In that case, the methods described in courses Slope Stability may be used to evaluate the stability of the foundation soils.
1.6.3 Estimation of Horizontal Movement of Abutments
The amount of horizontal movement the abutment may experience can also be estimated in design. Information from case histories for nine structures where measurements of abutment movements occurred is documented in Table 1-5.
The data presented in Table 1-5 provides a basis for estimating horizontal movement for abutments under similar conditions, provided a reasonable estimate of the post-construction fill settlement is made by using data from consolidation tests on high quality undisturbed Shelby tube samples. Note that the data for the abutments listed in Table 1-5 shows the horizontal movement (tilt) to range from 6 to 33% of the vertical fill settlement, with the average being 21%. Therefore, as a first approximation, it can be said that if the fill load exceeds the 3su limit prescribed by Equation 1-11, then the horizontal movement (tilt) of an abutment can be reasonably estimated as approximately 25% of the vertical fill settlement for the conditions listed in Table 1-5.

1.7 Design Solutions – Deformation Problems
Both the magnitude and time rate of settlement can affect fill structures, which in turn may affect the performance of other structures such as bridge abutments that are built within or in the vicinity of the fills. There are various methods to reduce the magnitude and time rate of settlement. All of these methods can be considered as ground improvement and are discussed in detail in FHWA (2006b). The reader is referred to FHWA (2006b) for further details. Solutions to prevent abutment tilting due to lateral squeeze are discussed in Section 1.7.3.
1.7.1 Reducing the Amount of Settlement
Settlement can be reduced by either increasing the resistance or reducing the load. Several ground improvement methods that are particularly suitable for reducing the amount of settlement are noted below.
1.7.1.1 Category 1 – Increasing the Resistance
Common ground improvement techniques that increase resistance include the following:
- Excavation and recompaction.
- Excavation and replacement.
- Vertical inclusions such as stone columns, shafts and piles. Embankments supported in this way are known as column supported embankments.
- Horizontal inclusions such as geosynthetics.
- Grouting, e.g., soil mixing, jet grouting.
- Dynamic compaction.
1.7.1.2 Category 2 – Reducing the Load
Common load reduction techniques include the following:
- Reduce grade line (reduction in height and/or flattening the slope)
- Use lightweight fill material, e.g., expanded shale, foamed concrete, geofoam.
- Bypass the soft layer with a deep foundation. Deep foundations may be used in conjunction with a load transfer platform (see FHWA 2006b).
1.7.2 Reducing Settlement Time
Often the major design consideration related to a settlement problem is the time for the settlement to occur. Low permeability clays and silty clays can take a long time to consolidate under an applied load. The settlement time is critical on most projects because it has a direct impact on construction schedules and delays increase project costs. Settlement time is also important to the maintenance personnel of a highway agency. The life cycle cost of annual regrading and resurfacing of settling roadways is usually far greater than the cost of design treatments to eliminate settlement before or during initial construction.
The two most common methods used to accelerate settlement and reduce settlement time are:
- Application of surcharge.
- Installation of vertical drains in the foundation soils.
Note that both of the above techniques lead to an increase in the resistance. These techniques are briefly discussed below and their use is illustrated in the Apple Freeway example in Appendix A.
1.7.2.1 Surcharge Treatment
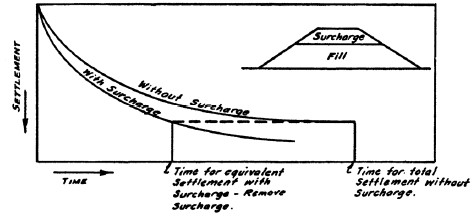
An embankment surcharge is constructed to a predetermined height, usually 1 to 10 ft (0.3 to 3 m) above final grade elevation based on settlement calculations. The surcharge is maintained for a predetermined waiting period (typically 3 to 12 months) based on settlement-time calculations. Depending upon the strength of the consolidating layer(s) the surcharge may have to be constructed in stages. The actual dimensions of the surcharge and the waiting period for each stage depend on the strength and drainage properties of the foundation soil as well as the initial height of the proposed embankment. The length of the waiting period can be estimated by using laboratory consolidation test data. The actual settlement occurring during embankment construction is then monitored with geotechnical instrumentation. When the settlement with surcharge equals the settlement originally estimated for the embankment, the surcharge is removed, as illustrated in Figure 1-21. If the surcharge is not removed after the desired amount of settlement has occurred, then additional settlement will continue to occur. Note that the stability of a surcharged embankment must be checked as part of the embankment design to ensure that an adequate short term safety factor exists. The stability is often field verified by monitoring with instrumentation such as inclinometers, piezometers and settlement points as discussed later.
1.7.2.2 Vertical Drains
Primary consolidation of some highly plastic clays can take many years to be completed. Surcharging alone may not be effective in reducing settlement time sufficiently since the longest distance to a drainage boundary may be significant. In such cases, vertical drains can be used to accelerate the settlement, either with or without surcharge treatment. The vertical drains accelerate the settlement rate by reducing the drainage path the water must travel to escape from the compressible soil layer to half the horizontal distance between drains, as illustrated in Figure 1-22. In most applications, a permeable sand blanket, 2 to 3 ft (0.6 to 1 m) thick, should be placed on the ground surface to permit free movement of water away from the embankment area and to create a working platform for installation of the drains. The drains are installed prior to placement of the embankment. The applied pressure from the embankment generates excess pore water pressure.
Recall that the consolidation time is proportional to the square of the length of the longest drainage path. Thus if the length of the drainage path is shortened by 50%, the consolidation time is reduced by a factor of four. Vertical drains and sand blankets should have high permeability to allow the water squeezed out of the subsoil to travel relatively quickly through the drains and the blanket.
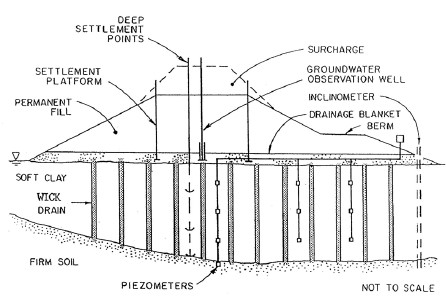
Wick drains are small prefabricated drains consisting of a plastic core that is wrapped with geotextile. Wick drains are typically 4 inches (100 mm) wide and about 1/4 inch (7 mm) thick. The drains are produced in rolls that can be fed into a mandrel. Wick drains are installed by pushing or vibrating a mandrel into the ground with the wick drain inside. When the bottom of the compressible soil is reached, the mandrel is withdrawn and the trimmed portion of the wick drain left in the ground. To minimize smear of the compressible soil, the cross-sectional area of the mandrel is recommended to be limited to a maximum of about 10 in2 (6,450 mm2). Predrilling of dense soil deposits may be required in some cases to reach the design depth. Use of wick drains in the United States began in the early 1970s. Design and construction guidance on the use of wick drains is provided in FHWA (1986, 2006b).
The feasibility of a surcharge solution should always be considered first since vertical drains are generally more expensive.
1.7.3 Design Solutions to Prevent Abutment Tilting
A recommended solution to minimize abutment-tilting is to induce settlement of the fill before the abutment piles or shafts are installed. If the construction time schedule or other factors do not permit pre-consolidation of the foundation soils before the piles or shafts are installed, then abutment tilting issues can be mitigated by the following design provisions:
- Use sliding plate expansion shoes large enough to accommodate the anticipated horizontal movement.
- Make provisions to fill in the bridge deck expansion joint over the abutment by inserting either metal plate fillers or larger neoprene joint fillers.
- Design the deep foundations for downdrag forces due to settlement. This solution does not improve the horizontal displacement effects.
- Use backward battered piles at the abutment and particularly at the wingwalls.
- Use lightweight fill materials to reduce driving forces
Displacements should also be monitored during and after construction so that the predicted movements can be compared to actual displacements. Displacements should be monitored by survey monuments or protected prisms installed on the face of the abutment and wingwalls and should be tied into permanent benchmarks.
1.8 Practical Aspects of Embankment Settlement
Few engineers realize the influence of embankment construction on the response of subsoils. The total weight of an embankment has an impact on the type of foundation treatment that may be appropriate. For instance, a relatively low height embankment of 10 ft (3 m) may be effectively surcharged because the additional surcharge weight could be 30 to 40 percent of the proposed embankment weight. However, when the embankment height exceeds 50 ft (15 m) the influence of a 5 or 10 ft (1.5 or 3 m) trapezoid of soil on top of this heavy 50 ft (15 m) mass is small and probably not cost-effective. Conversely, as the embankment height increases, the use of a shallow foundation for support of the abutment becomes more attractive. A 30 ft (9 m) high, 50 ft (15 m) long approach embankment weighs about 15,000 tons (130 MN) compared to the insignificant weight of a total (stub type) abutment loading that may equal 1,000 tons (9 MN). The width of an embankment also has an effect on total settlement. Wider embankments cause a pressure increase deeper into the subsoil. As might be expected, wider embankments may also cause more immediate and consolidation settlement and increase the time for consolidation to occur.
Recent developments in computer software readily permit computer analysis of approach embankment settlement. Programs such as FoSSA (2003), allow the user to compute settlements along abutments and to evaluate the effects of settlements on pipes buried in end slopes or pipes placed diagonally under approach fills.
1.9 Construction Monitoring and Quality Assurance
Approach embankment construction should be clearly defined in standard drawings as to materials and limits of placement. Such standards assure uniformity in construction due to the familiarity of the construction personnel with the operations being performed and results expected. Designers should attempt to use standard details wherever possible. Attempts at small changes in materials or limits are generally counterproductive to good construction where repetition of good practice is an important factor.
The philosophy of approach embankment details is to insure adequate bearing capacity for abutments or piers placed in the embankment and to minimize settlement of the pavement or footing. Typical highway embankments require compaction to 90 percent of maximum dry density (AASHTO T180) to control pavement settlement. Designers should specify materials and compaction control as shown in Figure 1-4, to limit differential settlement between the structure and approach fill. If piles are used to support footings in fill, the largest particle size of embankment material should be limited to 6 in (150 mm) to ease pile installation either by driving or pre-drilling. If spread footings are used, a minimum of 5 ft (1.5 m) of select material compacted to 100 percent of maximum dry density (AASHTO T99) should be placed beneath the footing and extended beyond the wingwalls. This layer provides uniform support for the footing and a rigid transition between the structure and the fill to minimize differential settlement. Construction control is usually referenced to percent compaction on the standard design drawings.
1.9.1 Embankment Construction Monitoring by Instrumentation
The observational approach to design involves monitoring subsoil behavior during early construction stages to verify design and to predict responses to subsequent construction. Basic soil mechanics concepts can be used to predict future subsoil behavior accurately if data from instrumentation are analyzed after initial construction loads have been placed. Occasionally a design problem arises that is unique or extremely critical and that can be safely solved only by utilizing the observational approach.
Embankment placement must be carefully observed and monitored on projects where stability and/or settlement are critical. The monitoring should include visual observation by the construction inspection staff and the use of instrumentation. Without the aid of various forms of instrumentation, it is impossible to determine accurately what is happening to the foundation. Instrumentation can be used to warn of imminent failure or to indicate whether settlement is occurring as predicted. The type of instruments to be used and where they will be placed should be planned by a qualified and experienced geotechnical specialist. Actual interpretation and analysis of the data should also be performed by someone with a background in soil mechanics; however, the project engineer and inspector should understand the purpose of each type of instrumentation and how the data are to be used.
1.9.1.1 Inspector’s Visual Observation
In areas of marginal embankment stability, the inspector should walk the surface of the embankment daily looking for any sign of cracking or movement. Hairline cracks often develop at the embankment surface just prior to failure. If the inspector discovers any such features, all fill operations should cease immediately. All instrumentation should be read immediately. The geotechnical specialist should be notified. Subsequent readings will indicate when it is safe to resume operations. Unloading by removal of fill material or other mitigation methods are sometimes necessary to prevent an embankment failure.
1.9.1.2 Types of Instrumentation
The typical instrumentation specified to monitor foundation performance on projects where stability and settlement are critical consists of:
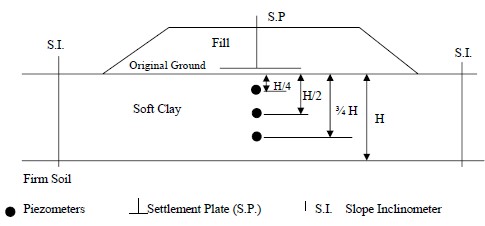
- Slope Inclinometers are used to monitor subsurface lateral deformation. A slope inclinometer typically consists of a 3 in (75 mm) internal diameter (ID) plastic tube with four grooves cut at 90-degree intervals around the inside. The slope inclinometer tube is installed in a borehole. The bottom of the slope inclinometer tube must be founded in firm soil or rock. A readout probe that fits into the grooves is lowered down the tube and angular deflection of the tube is measured. The amount and location of horizontal movement in the foundation soil can then be measured. For embankments built over very soft subsoils, telescoping inclinometer casing should be used to account for vertical consolidation. In soft ground conditions, several inches of lateral movement due to squeeze may occur without shear failure as the embankment is built. Therefore, from a practical construction control standpoint, the rate of movement rather than the amount is the better indicator of imminent failure. Slope inclinometer readings should be made often during the critical embankment placement period, daily if fill placement is proceeding rapidly, and readings should be plotted immediately on a movement versus time plot. Fill operations should cease if a sudden increase in the rate of movement occurs.
- Piezometers indicate the amount of excess pressure build-up within the water-saturated pores of the soil. There are critical levels to which the water pressure in the subsoil will increase just prior to failure. The geotechnical specialist can estimate the critical water pressure level during design. Normally, the primary function of piezometers during fill placement is to warn of failures. Once the embankment placement is complete, the piezometers are used to measure the rate of consolidation. There are several different types of piezometers. The simplest is the open standpipe type, which is essentially a well point with a metal or plastic pipe attached to it. The pipe is extended up through the fill in sections as the fill height increases. This type of open well piezometer has the disadvantage that the pipes are susceptible to damage if hit by construction equipment. Also, the response time of open well piezometers is often too slow in soft clays to warn of potential embankment failure. There are several types of remote piezometers that eliminate the requirement for extending a pipe up through the fill. The remote units consist of a piezometer transducer that is sealed in a borehole with leads carried out laterally under the base of the embankment to a readout device that records the pore water pressure measured by the transducer. Pneumatic or vibrating wire piezometers have a more rapid response to changes in pore water pressure than open-stand pipe piezometers.
- Settlement devices are used to measure the amount and rate of settlement of the foundation soil due to the load from the embankment. Typically they are installed on or just below the existing ground surface before any fill is placed. The simplest settlement device is a settlement plate usually a 3 or 4 ft (0.9 to 1.2 m square plywood mat or steel plate with a vertical reference rod (usually ¾ in (19 mm) pipe) attached to the plate. The reference rods are normally added 4 ft (1.2 m) at a time as the height of the embankment increases. The elevation of the top of the reference rod is surveyed periodically to measure the foundation settlement. Remote pneumatic settlement devices are also available. As with the remote piezometer devices, the remote settlement devices have the advantage of not having a reference rod extending up through the fill.
1.9.1.3 Typical Locations for Instruments
Instrument installations should be spaced approximately 250 to 500 ft (75 to 150 m) along the roadway alignment in critical areas. Typical locations of instruments for an embankment over soft ground are shown in Figure 1-23: