Chapter: 1 A Brief History

Introduction

The houses in the past were built to keep the rain, snow, and thieves out with hardly any attention given to heat losses and energy conservation. Houses had little or no insulation, and the structures had numerous cracks through which air leaked. We have seen dramatic changes in the construction of residential and commercial buildings in the 20th century as a result of increased awareness of limited energy resources together with the escalating energy prices and the demand for a higher level of thermal comfort. Today, most local codes specify the minimum level of insulation to be used in the walls and the roof of new houses, and often require the use of double-pane windows. As a result, today’s houses are well insulated, weatherproofed, and nearly air tight, and provide better thermal comfort.

The failures and successes of the past often shed light to the future, and thus we start this chapter with a brief history of heating and cooling to put things into historical perspective. Then we discuss the criteria for thermal comfort, which is the primary reason for installing heating and cooling systems. In the remainder of the chapter, we present calculation procedures for the heating and cooling loads of buildings using the most recent information and design criteria established by the American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. (ASHRAE), which publishes and periodically revises the most authoritative handbooks in the field. This chapter is in- tended to introduce the readers to an exciting application area of heat transfer, and to help them develop a deeper understanding of the fundamentals of heat transfer using this familiar setup. The reader is referred to ASHRAE hand- books for more information.

A Brief History

Unlike animals such as a fox or a bear that are born with built-in furs, human beings come into this world with little protection against the harsh environmental conditions (Fig. 1). Therefore, we can claim that the search for thermal comfort dates back to the beginning of human history. It is believed that early human beings lived in caves that provided shelter as well as protection from extreme thermal conditions. Probably the first form of heating system used was open fire, followed by fire in dwellings through the use of a chimney to vent out the combustion gases. The concept of central heating dates back to the times of the Romans, who heated homes by utilizing double-floor construction techniques and passing the fire’s fumes through the opening between the two floor layers. The Romans were also the first to use transparent windows made of mica or glass to keep the wind and rain out while letting the light in. Wood and coal were the primary energy sources for heating, and oil and candles were used for lighting. The ruins of south-facing houses indicate that the value of solar heating was recognized early in the history.

The development of the first steam heating system by James Watt dates back to 1770. When the American Society of Heating and Ventilating Engineers was established in New York in 1894, central heating systems using cast iron warm air furnaces and boilers were in common use. Fans were added in 1899 to move the air mechanically, and later automatic firing replaced the manual firing. The steam heating systems gained widespread acceptance in the early 1900’s by the introduction of fluid-operated thermostatic traps to improve the fluid circulation. Gravity-driven hot water heating systems were developed in parallel with steam systems. Suspended and floor-type unit heaters, unit ventilators, and panel heaters were developed in the 1920’s. Unit heaters and panel heaters usually used steam, hot water, or electricity as the heat source. It became common practice to conceal the radiators in the 1930’s, and the baseboard radiator was developed in 1944. Today, air heating systems with a duct distribution network dominate the residential and commercial buildings.

The development of cooling systems took the back seat in the history of thermal comfort since there was no quick way of creating “coolness.” Therefore, early attempts at cooling were passive measures such as blocking off direct sunlight and using thick stone walls to store coolness at night. A more sophisticated approach was to take advantage of evaporation cooling by running water through the structure, as done in the Alhambra castle. Of course, natural ice and snow served as “cold storage” mediums and provided some cooling. In 1775, Dr. William Cullen made ice in Scotland by evacuating the air in a water tank (Fig. 2). It was also known at those times that some chemicals lowered temperatures. For example, the temperature of snow can be dropped to 33C (27F) by mixing it with calcium chloride. This process was commonly used to make ice cream. In 1851, Ferdinand Carre designed the first ammonia absorption refrigeration system, while Dr. John Gorrie received a patent for an open air refrigeration cycle to produce ice and refrigerated air. In 1853, Alexander Twining of Connecticut produced 1600 pounds (726 kg) of ice a day using sulfuric ether as the refrigerant. In 1872, David Boyle developed an ammonia compression machine that produced ice. Mechanical refrigeration at those times was used primarily to make ice and preserve perishable commodities such as meat and fish (Sauer and Howell, 1994).

Comfort cooling was obtained by ice or by chillers that used ice. Air cooling systems for thermal comfort were built in the 1890’s, but they did not find widespread use until the development of mechanical refrigeration in the early 1900’s. In 1905, 200 Btu/min (or 12,000 Btu/h) was established as 1 ton of refrigeration, and in 1902 a 400-ton air-conditioning system was installed in the New York Stock Exchange. The system operated reliably for 20 years. A modern air-conditioning system was installed in the Boston Floating Hospital in 1908, which was a first for a hospital. In a monumental paper presented in 1911, Willis Carrier (1876–1950), known as the “Father of Air Conditioning,” laid out the formulas related to the dry-bulb, wet-bulb, and dew-point temperatures of air and the sensible, latent, and total heat loads. By 1922, the centrifugal refrigeration machine developed by Carrier made water chilling for medium and large commercial and industrial facilities practical and economical. In 1928 the Milan Building in San Antonio, Texas, was the first commercial building designed with and built for comfort air-conditioning specifications (Sauer and Howell, 1994).

Frigidaire introduced the first room air conditioner in the late 1920’s (Fig. 3). The halocarbon refrigerants such as Freon-12 were developed in 1930. The concept of a heat pump was described by Sadi Carnot in 1824, and the operation of such a device called the “heat multiplier” was first described by William Thomson (Lord Kelvin) in 1852. T. G. N. Haldane built an experimental heat pump in 1930, and a heat pump was marketed by De La Vargne in 1933. General Electric introduced the heat pump in the mid 1930’s, and heat pumps were being mass produced in 1952. Central air-conditioning systems were being installed routinely in the 1960’s. The oil crises of the 1970’s sent shock waves among the consumers and the producers of energy-consuming equipment, which had taken energy for granted, and brought about a renewed interest in the development of energy-efficient systems and more effective insulation materials. Today most residential and commercial buildings are equipped with modern air-conditioning systems that can heat, cool, humidify, dehumidify, clean, and even deodorize the air—in other words, condition the air to people’s desires.

Chapter: 2 Human Body and Thermal Comfort

The term air-conditioning is usually used in a restricted sense to imply cooling, but in its broad sense it means to condition the air to the desired level by heating, cooling, humidifying, dehumidifying, cleaning, and deodorizing. The purpose of the air-conditioning system of a building is to provide complete thermal comfort for its occupants. Therefore, we need to understand the thermal aspects of the human body in order to design an effective air-conditioning system.

The building blocks of living organisms are cells, which resemble miniature factories performing various functions necessary for the survival of organisms. The human body contains about 100 trillion cells with an average diameter of 0.01 mm. In a typical cell, thousands of chemical reactions occur every second during which some molecules are broken down and energy is released and some new molecules are formed. The high level of chemical activity in the cells that maintain the human body temperature at a temperature of 37.0C (98.6F) while performing the necessary bodily functions is called the metabolism. In simple terms, metabolism refers to the burning of foods such as carbohydrates, fat, and protein. The metabolizable energy content of foods is usually expressed by nutritionists in terms of the capitalized Calorie. One Calorie is equivalent to 1 Cal = 1 kcal = 4.1868 kJ.

The rate of metabolism at the resting state is called the basal metabolic rate, which is the rate of metabolism required to keep a body performing the necessary bodily functions such as breathing and blood circulation at zero external activity level. The metabolic rate can also be interpreted as the energy consumption rate for a body. For an average man (30 years old, 70 kg, 1.73 m high, 1.8 m2 surface area), the basal metabolic rate is 84 W. That is, the body is converting chemical energy of the food (or of the body fat if the person had not eaten) into heat at a rate of 84 J/s, which is then dissipated to the surroundings. The metabolic rate increases with the level of activity, and it may exceed 10 times the basal metabolic rate when someone is doing strenuous exercise. That is, two people doing heavy exercising in a room may be supplying more energy to the room than a 1-kW resistance heater (Fig. 4). An average man generates heat at a rate of 108 W while reading, writing, typing, or listening to a lecture in a classroom in a seated position. The maximum metabolic rate of an average man is 1250 W at age 20 and 730 at age 70. The corresponding rates for women are about 30 percent lower. Maximum metabolic rates of trained athletes can exceed 2000 W.

Metabolic rates during various activities are given in Table 1 per unit body surface area. The surface area of a nude body was given by D. DuBois in 1916 as 

where m is the mass of the body in kg and h is the height in m. Clothing increases the exposed surface area of a person by up to about 50 percent. The metabolic rates given in the table are sufficiently accurate for most purposes, but there is considerable uncertainty at high activity levels. More accurate values can be determined by measuring the rate of respiratory oxygen consumption, which ranges from about 0.25 L/min for an average resting man to more than 2 L/min during extremely heavy work. The entire energy released during metabolism can be assumed to be released as heat (in sensible or latent forms) since the external mechanical work done by the muscles is very small. Besides, the work done during most activities such as walking or riding an exercise bicycle is eventually converted to heat through friction.

The comfort of the human body depends primarily on three environmental factors: the temperature, relative humidity, and air motion. The temperature of the environment is the single most important index of comfort. Extensive research is done on human subjects to determine the “thermal comfort zone” and to identify the conditions under which the body feels comfortable in an environment. It has been observed that most normally clothed people resting or doing light work feel comfortable in the operative temperature (roughly, the average temperature of air and surrounding surfaces) range of 23 to 27C or 73 to 80F (Fig. 5). For unclothed people, this range is 29 to 31C. Relative humidity also has a considerable effect on comfort since it is a measure of air’s ability to absorb moisture and thus it affects the amount of heat a body can dissipate by evaporation. High relative humidity slows down heat rejection by evaporation, especially at high temperatures, and low relative humidity speeds it up. The desirable level of relative humidity is the broad range of 30 to 70 percent, with 50 percent being the most desirable level. Most people at these conditions feel neither hot nor cold, and the body does not need to activate any of the defense mechanisms to maintain the normal body temperature (Fig. 6)

Another factor that has a major effect on thermal comfort is excessive air motion or draft, which causes undesired local cooling of the human body. Draft is identified by many as a most annoying factor in work places, automobiles, and airplanes. Experiencing discomfort by draft is most common among people wearing indoor clothing and doing light sedentary work, and least common among people with high activity levels. The air velocity should be kept below 9 m/min (30 ft/min) in winter and 15 m/min (50 ft/min) in summer to minimize discomfort by draft, especially when the air is cool. A low level of air motion is desirable as it removes the warm, moist air that builds around the body and replaces it with fresh air. Therefore, air motion should be strong enough to remove heat and moisture from the vicinity of the body, but gentle enough to be unnoticed. High speed air motion causes discomfort outdoors as well. For example, an environment at 10C (50F) with 48 km/h winds feels as cold as an environment at 7C (20F) with 3 km/h winds because of the chilling effect of the air motion (the wind-chill factor).

A comfort system should provide uniform conditions throughout the living space to avoid discomfort caused by nonuniformities such as drafts, asymmetric thermal radiation, hot or cold floors, and vertical temperature stratification. Asymmetric thermal radiation is caused by the cold surfaces of large windows, uninsulated walls, or cold products and the warm surfaces of gas or electric radiant heating panels on the walls or ceiling, solar-heated masonry walls or ceilings, and warm machinery. Asymmetric radiation causes discomfort by exposing different sides of the body to surfaces at different temperatures and thus to different heat loss or gain by radiation. A person whose left side is exposed to a cold window, for example, will feel like heat is being drained from that side of his or her body (Fig. 7). For thermal comfort, the radiant temperature asymmetry should not exceed 5C in the vertical direction and 10C in the horizontal direction. The unpleasant effect of radiation asymmetry can be minimized by properly sizing and installing heating panels, using double-pane windows, and providing generous insulation at the walls and the roof.

Direct contact with cold or hot floor surfaces also causes localized discomfort in the feet. The temperature of the floor depends on the way it is constructed (being directly on the ground or on top of a heated room, being made of wood or concrete, the use of insulation, etc.) as well as the floor covering used such as pads, carpets, rugs, and linoleum. A floor temperature of 23 to 25C is found to be comfortable to most people. The floor asymmetry loses its significance for people with footwear. An effective and economical way of raising the floor temperature is to use radiant heating panels instead of turning the thermostat up. Another nonuniform condition that causes discomfort is temperature stratification in a room that exposes the head and the feet to different temperatures. For thermal comfort, the temperature difference between the head and foot levels should not exceed 3C. This effect can be minimized by using destratification fans.

It should be noted that no thermal environment will please everyone. No matter what we do, some people will express some discomfort. The thermal comfort zone is based on a 90 percent acceptance rate. That is, an environment is deemed comfortable if only 10 percent of the people are dissatisfied with it. Metabolism decreases somewhat with age, but it has no effect on the comfort zone. Research indicates that there is no appreciable difference between the environments preferred by old and young people. Experiments also show that men and women prefer almost the same environment. The metabolism rate of women is somewhat lower, but this is compensated by their slightly lower skin temperature and evaporative loss. Also, there is no significant variation in the comfort zone from one part of the world to another and from winter to summer. Therefore, the same thermal comfort conditions can be used throughout the world in any season. Also, people cannot acclimatize themselves to prefer different comfort conditions.

In a cold environment, the rate of heat loss from the body may exceed the rate of metabolic heat generation. Average specific heat of the human body is 3.49 kJ/kg · C, and thus each 1C drop in body temperature corresponds to a deficit of 244 kJ in body heat content for an average 70 kg man. A drop of 0.5C in mean body temperature causes noticeable but acceptable discomfort. A drop of 2.6C causes extreme discomfort. A sleeping person will wake up when his or her mean body temperature drops by 1.3C (which normally shows up as a 0.5C drop in the deep body and 3C in the skin area). The drop of deep body temperature below 35C may damage the body temperature regulation mechanism, while a drop below 28C may be fatal. Sedentary people reported to feel comfortable at a mean skin temperature of 33.3C, uncomfortably cold at 31C, shivering cold at 30C, and extremely cold at 29C. People doing heavy work reported to feel comfortable at much lower temperatures, which shows that the activity level affects human performance and comfort. The extremities of the body such as hands and feet are most easily affected by cold weather, and their temperature is a better indication of comfort and performance. A hand-skin temperature of 20C is perceived to be uncomfortably cold, 15C to be extremely cold, and 5C to be painfully cold. Useful work can be performed by hands without difficulty as long as the skin temperature of fingers remains above 16C (ASHRAE Handbook of Fundamentals, Chap. 8).

The first line of defense of the body against excessive heat loss in a cold environment is to reduce the skin temperature and thus the rate of heat loss from the skin by constricting the veins and decreasing the blood flow to the skin. This measure decreases the temperature of the tissues subjacent to the skin, but maintains the inner body temperature. The next preventive measure is increasing the rate of metabolic heat generation in the body by shivering, unless the person does it voluntarily by increasing his or her level of activity or puts on additional clothing. Shivering begins slowly in small muscle groups and may double the rate of metabolic heat production of the body at its initial stages. In the extreme case of total body shivering, the rate of heat production may reach 6 times the resting levels (Fig. 8). If this measure also proves inadequate, the deep body temperature starts falling. Body parts furthest away from the core such as the hands and feet are at greatest danger for tissue damage.

In hot environments, the rate of heat loss from the body may drop below the metabolic heat generation rate. This time the body activates the opposite mechanisms. First the body increases the blood flow and thus heat transport to  the skin, causing the temperature of the skin and the subjacent tissues to rise and approach the deep body temperature. Under extreme heat conditions, the heart rate may reach 180 beats per minute in order to maintain adequate blood supply to the brain and the skin. At higher heart rates, the volumetric efficiency of the heart drops because of the very short time between the beats to fill the heart with blood, and the blood supply to the skin and more importantly to the brain drops. This causes the person to faint as a result of heat exhaustion. Dehydration makes the problem worse. A similar thing happens when a person working very hard for a long time stops suddenly. The blood that has flooded the skin has difficulty returning to the heart in this case since the relaxed muscles no longer force the blood back to the heart, and thus there is less blood available for pumping to the brain.

The next line of defense is releasing water from sweat glands and resorting to evaporative cooling, unless the person removes some clothing and reduces the activity level (Fig. 9). The body can maintain its core temperature at 37C in this evaporative cooling mode indefinitely, even in environments at higher temperatures (as high as 200C during military endurance tests), if the person drinks plenty of liquids to replenish his or her water reserves and the ambient air is sufficiently dry to allow the sweat to evaporate instead of rolling down the skin. If this measure proves inadequate, the body will have to start absorbing the metabolic heat and the deep body temperature will rise. A person can tolerate a temperature rise of 1.4C without major discomfort but may collapse when the temperature rise reaches 2.8C. People feel sluggish and their efficiency drops considerably when the core body temperature rises above 39C. A core temperature above 41C may damage hypothalamic proteins, resulting in cessation of sweating, increased heat production by shivering, and a heat stroke with an irreversible and life-threatening damage. Death can occur above 43C.

A surface temperature of 46°C causes pain on the skin. Therefore, direct contact with a metal block at this temperature or above is painful. However, a person can stay in a room at 100°C for up to 30 min without any damage or pain on the skin because of the convective resistance at the skin surface and evaporative cooling. We can even put our hands into an oven at 200°C for a short time without getting burned.

Another factor that affects thermal comfort, health, and productivity is ventilation. Fresh outdoor air can be provided to a building naturally by doing nothing, or forcefully by a mechanical ventilation system. In the first case, which is the norm in residential buildings, the necessary ventilation is provided by infiltration through cracks and leaks in the living space and by the opening of the windows and doors. The additional ventilation needed in the bathrooms and kitchens is provided by air vents with dampers or exhaust fans. With this kind of uncontrolled ventilation, however, the fresh air supply will be either too high, wasting energy, or too low, causing poor indoor air quality. But the current practice is not likely to change for residential buildings since there is not a public outcry for energy waste or air quality, and thus it is difficult to justify the cost and complexity of mechanical ventilation systems.

Mechanical ventilation systems are part of any heating and air-conditioning system in commercial buildings, providing the necessary amount of fresh out- door air and distributing it uniformly throughout the building. This is not sur- prising since many rooms in large commercial buildings have no windows and thus rely on mechanical ventilation. Even the rooms with windows are in the same situation since the windows are tightly sealed and cannot be opened  in most buildings. It is not a good idea to oversize the ventilation system just to be on the “safe side” since exhausting the heated or cooled indoor air wastes energy. On the other hand, reducing the ventilation rates below the required minimum to conserve energy should also be avoided so that the indoor air quality can be maintained at the required levels. The minimum fresh air ven- tilation requirements are listed in Table 2. The values are based on con- trolling the CO₂ and other contaminants with an adequate margin of safety, which requires each person be supplied with at least 7.5 L/s (15 ft3/min) of fresh air.

Another function of the mechanical ventilation system is to clean the air by filtering it as it enters the building. Various types of filters are available for this purpose, depending on the cleanliness requirements and the allowable pressure drop.

Chapter: 3 Heat Transfer from the Human Body

The metabolic heat generated in the body is dissipated to the environment through the skin and the lungs by convection and radiation as sensible heat and by evaporation as latent heat (Fig. 10). Latent heat represents the heat of vaporization of water as it evaporates in the lungs and on the skin by absorbing body heat, and latent heat is released as the moisture condenses on cold surfaces. The warming of the inhaled air represents sensible heat transfer in the lungs and is proportional to the temperature rise of inhaled air. The total rate of heat loss from the body can be expressed as

Therefore, the determination of heat transfer from the body by analysis alone is difficult. Clothing further complicates the heat transfer from the body, and thus we must rely on experimental data. Under steady conditions, the total rate of heat transfer from the body is equal to the rate of metabolic heat generation in the body, which varies from about 100 W for light office work to roughly 1000 W during heavy physical work.

Sensible heat loss from the skin depends on the temperatures of the skin, the environment, and the surrounding surfaces as well as the air motion. The latent heat loss, on the other hand, depends on the skin wettedness and the relative humidity of the environment as well. Clothing serves as insulation and reduces both the sensible and latent forms of heat loss. The heat transfer from the lungs through respiration obviously depends on the frequency of breathing and the volume of the lungs as well as the environmental factors that affect heat transfer from the skin.

Sensible heat from the clothed skin is first transferred to the clothing and then from the clothing to the environment. The convection and radiation heat losses from the outer surface of a clothed body can be expressed as

The convection heat transfer coefficients at 1 atm pressure are given in  Table 3. Convection coefficients at pressures P other than 1 atm are obtained by multiplying the values at atmospheric pressure by P 0.55 where P is in atm. Also, it is recognized that the temperatures of different surfaces surrounding a person are probably different, and T_surr represents the mean radiation temperature, which is the temperature of an imaginary isothermal enclosure in which radiation heat exchange with the human body equals the radiation heat exchange with the actual enclosure. Noting that most clothing and building materials are very nearly black, the mean radiation temperature of an enclosure that consists of N surfaces at different temperatures can be determined from

where T_i is the temperature of the surface i and F_person-i is the view factor between the person and surface i. Total sensible heat loss can also be expressed conveniently by combining the convection and radiation heat losses as

where the operative temperature T_operative is the average of the mean radiant and ambient temperatures weighed by their respective convection and radiation heat transfer coefficients and is expressed as (Fig. 11)

Note that the operative temperature will be the arithmetic average of the ambient and surrounding surface temperatures when the convection and radiation heat transfer coefficients are equal to each other. Another environmental index used in thermal comfort analysis is the effective temperature, which combines the effects of temperature and humidity. Two environments with the same effective temperature evokes the same thermal response in people even though they are at different temperatures and humidities. Heat transfer through the clothing can be expressed as

where R_clothing is the unit thermal resistance of clothing in m2 · °C/W, which involves the combined effects of conduction, convection, and radiation between the skin and the outer surface of clothing. The thermal resistance of clothing is usually expressed in the unit clo where 1 clo = 0.155 m2 · °C/W = 0.880 ft2 · °F · h/Btu. The thermal resistance of trousers, long-sleeve shirt, long-sleeve sweater, and T-shirt is 1.0 clo, or 0.155 m2 · °C/W. Summer clothing such as light slacks and short-sleeved shirt has an insulation value of 0.5 clo, whereas winter clothing such as heavy slacks, long-sleeve shirt, and a sweater or jacket has an insulation value of 0.9 clo. Then the total sensible heat loss can be expressed in terms of the skin temperature instead of the inconvenient clothing temperature as (Fig. 12)

At a state of thermal comfort, the average skin temperature of the body is observed to be 33°C (91.5°F). No discomfort is experienced as the skin temperature fluctuates by ±1.5°C (2.5°F). This is the case whether the body is clothed or unclothed.

Evaporative or latent heat loss from the skin is proportional to the difference between the water vapor pressure at the skin and the ambient air, and the skin wettedness, which is a measure of the amount of moisture on the skin. It is due to the combined effects of the evaporation of sweat and the diffusion of water through the skin, and can be expressed as

Heat loss by evaporation is maximum when the skin is completely wetted. Also, clothing offers resistance to evaporation, and the rate of evaporation in clothed bodies depends on the moisture permeability of the clothes. The maximum evaporation rate for an average man is about 1 L/h (0.3 g/s), which rep- resents an upper limit of 730 W for the evaporative cooling rate. A person can lose as much as 2 kg of water per hour during a workout on a hot day, but any excess sweat slides off the skin surface without evaporating (Fig. 13).

During respiration, the inhaled air enters at ambient conditions and exhaled air leaves nearly saturated at a temperature close to the deep body temperature (Fig. 14). Therefore, the body loses both sensible heat by convection and latent heat by evaporation from the lungs, and these can be expressed as

T# he rate of air intake to the lungs is directly proportional to the metabolic rate Q_met. The rate of total heat loss from the lungs through respiration can be expressed approximately as

where P_{v, ambient} is the vapor pressure of ambient air in kPa.

The fraction of sensible heat varies from about 40 percent in the case of heavy work to about 70 percent during light work. The rest of the energy is rejected from the body by perspiration in the form of latent heat.

Chapter: 4 Design Conditions for Heating and Cooling

The size of a heating or cooling system for a building is determined on the basis of the desired indoor conditions that must be maintained based on the outdoor conditions that exist at that location. The desirable ranges of temperatures, humidities, and ventilation rates (the thermal comfort zone) discussed earlier constitute the typical indoor design conditions, and they remain fairly constant. For example, the recommended indoor temperature for general com- fort heating is 22°C (or 72°F). The outdoor conditions at a location, on the other hand, vary greatly from year to year, month to month, and even hour to hour. The set of extreme outdoor conditions under which a heating or cooling system must be able to maintain a building at the indoor design conditions is called the outdoor design conditions (Fig. 17).

When designing a heating, ventilating, and air-conditioning (HVAC) system, perhaps the first thought that comes to mind is to select a system that is large enough to keep the indoors at the desired conditions at all times even under the worst weather conditions. But sizing an HVAC system on the basis of the most extreme weather on record is not practical since such an oversized system will have a higher initial cost, will occupy more space, and will prob- ably have a higher operating cost because the equipment in this case will run at partial load most of time and thus at a lower efficiency. Most people would not mind experiencing an occasional slight discomfort under extreme weather conditions if it means a significant reduction in the initial and operating costs of the heating or cooling system. The question that arises naturally is what is a good compromise between economics and comfort?

To answer this question, we need to know what the weather will be like in the future. But even the best weather forecasters cannot help us with that. Therefore, we turn to the past instead of the future and bet that the past weather data averaged over several years will be representative of a typical year in the future. The weather data in Tables 4 and 5 are based on the records of numerous weather stations in the United States that recorded the 97.5 percent winter design temperature for Denver, Colorado, is -17°C, and thus the temperatures in Denver may fall below -17°C about 2.5 percent of the time during winter months in a typical year. Critical applications such as health care facilities and certain process industries may require the more stringent 99 percent level.

Table 4 lists the outdoor design conditions for both cases as well as summer comfort levels. The winter percentages are based on the weather data for the months of December, January, and February while the summer percent- ages are based on the four months June through September. The three winter months have a total of 31 + 31 + 28 = 90 days and thus 2160 hours. There- fore, the conditions of a house whose heating system is based on the 97.5 per- cent level may fall below the comfort level for 2160 X 2.5% = 54 hours during the heating season of a typical year. However, most people will not even notice it because everything in the house will start giving off heat as soon as the temperature drops below the thermostat setting. This is especially the case in buildings with large thermal masses. The minimum temperatures usu- ally occur between 6:00 _AM and 8:00 _AM solar time, and thus commercial buildings that open late (such as shopping centers) may even use less stringent outdoor design conditions (such as the 95 percent level) for their heating systems. This is also the case with the cooling systems of residences that are unoccupied during the maximum temperatures, which occur between 2:00 _PM and 4:00 _PM solar time in the summer.

The heating or cooling loads of a building represent the heat that must be supplied to or removed from the interior of a building to maintain it at the desired conditions. A distinction should be made between the design load and the actual load of heating or cooling systems. The design (or peak) heating load is usually determined with a steady-state analysis using the design conditions for the indoors and the outdoors for the purpose of sizing the heating system (Fig. 19). This ensures that the system has the required capacity to perform adequately at the anticipated worst conditions. But the energy use of a building during a heating or cooling season is determined on the basis of the actual heating or cooling load, which varies throughout the day.

The internal heat load (the heat dissipated off by people, lights, and appliances in a building) is usually not considered in the determination of the design heating load but is considered in the determination of the design cool- ing load. This is to ensure that the heating system selected can heat the building even when there is no contribution from people or appliances, and the cooling system is capable of cooling it even when the heat given off by people and appliances is at its highest level.

Wind increases heat transfer to or from the walls, roof, and windows of a building by increasing the convection heat transfer coefficient and also increasing the infiltration. Therefore, wind speed is another consideration when determining the heating and cooling loads. The recommended values of wind speed to be considered are 15 mph (6.7 m/s) for winter and 7.5 mph (3.4 m/s) for summer. The corresponding design values recommended by ASHRAE for heat transfer coefficients for combined convection and radiation on the outer surface of a building are

The recommended heat transfer coefficient value for the interior surfaces of a building for both summer and winter is (Fig. 20)

For well-insulated buildings, the surface heat transfer coefficients constitute a small part of the overall heat transfer coefficients, and thus the effect of possible deviations from the above values is usually insignificant.

In summer, the moisture level of the outdoor air is much higher than that of indoor air. Therefore, the excess moisture that enters a house from the outside with infiltrating air needs to be condensed and removed by the cooling system. But this requires the removal of the latent heat from the moisture, and the cooling system must be large enough to handle this excess cooling load. To size the cooling system properly, we need to know the moisture level of    the outdoor air at design conditions. This is usually done by specifying the wet-bulb temperature, which is a good indicator of the amount of moisture in the air. The moisture level of the cold outside air is very low in winter, and thus normally it does not affect the heating load of a building.

Solar radiation plays a major role on the heating and cooling of buildings, and you may think that it should be an important consideration in the evaluation of the design heating and cooling loads. Well, it turns out that peak heating loads usually occur early in the mornings just before sunrise. Therefore, solar radiation does not affect the peak or design heating load and thus the size of a heating system. However, it has a major effect on the actual heating load, and solar radiation can reduce the annual heating energy consumption of a building considerably.

Sol-Air Temperature

The sun is the main heat source of the earth, and without the sun, the environment temperature would not be much higher than the deep space temperature of -270°C. The solar energy stored in the atmospheric air, the ground, and the structures such as buildings during the day is slowly released at night, and thus the variation of the outdoor temperature is governed by the incident solar radiation and the thermal inertia of the earth. Heat gain from the sun is the primary reason for installing cooling systems, and thus solar radiation has a major effect on the peak or design cooling load of a building, which usually occurs early in the afternoon as a result of the solar radiation entering through the glazing directly and the radiation absorbed by the walls and the roof that is released later in the day.

The effect of solar radiation for glazing such as windows is expressed in terms of the solar heat gain factor (SHGF), discussed later in this chapter. For opaque surfaces such as the walls and the roof, on the other hand, the effect of solar radiation is conveniently accounted for by considering the outside temperature to be higher by an amount equivalent to the effect of solar radiation. This is done by replacing the ambient temperature in the heat transfer relation through the walls and the roof by the sol-air temperature, which is defined as the equivalent outdoor air temperature that gives the same rate of heat transfer to a surface as would the combination of incident solar radiation, convection with the ambient air, and radiation exchange with the sky and the surrounding surfaces (Fig.22).

Heat flow into an exterior surface of a building subjected to solar radiation can be expressed as

where a_s is the solar absorptivity and e is the emissivity of the surface, h_o is the combined convection and radiation heat transfer coefficient, q·solar is the so- lar radiation incident on the surface (in W/m2 or Btu/h · ft2) and

is the sol-air temperature. The first term in Equation 16–15 represents the convection and radiation heat transfer to the surface when the average surrounding surface and sky temperature is equal to the ambient air temperature,   T_surr = T_ambient, and the last term represents the correction for the radiation heat transfer when T_surr -:: T_ambient. The last term in the sol-air temperature relation represents the equivalent change in the ambient temperature corresponding to this radiation correction effect and ranges from about zero for vertical wall surfaces to 4°C (or 7°F) for horizontal or inclined roof surfaces facing the sky. This difference is due to the low effective sky temperature.

The sol-air temperature for a surface obviously depends on the absorptivity of the surface for solar radiation, which is listed in Table 6 for common exterior surfaces. Being conservative and taking h_o = 17 W/m2 · °C = 3.0 Btu/h · ft2 · °F, the summer design values of the ratio a_s/h_o for light- and dark-colored surfaces are determined to be (Fig. 23)

where we have assumed conservative values of 0.45 and 0.90 for the solar absorptivities of light- and dark-colored surfaces, respectively. The sol-air temperatures for light- and dark-colored surfaces are listed in Table 7 for July 21 at 40° N latitude versus solar time. Sol-air temperatures for other dates and latitudes can be determined from Equation 16–16 by using appropriate temperature and incident solar radiation data.

Once the sol-air temperature is available, heat transfer through a wall (or similarly through a roof ) can be expressed as

where A_s is the wall area and U is the overall heat transfer coefficient of the wall. Therefore, the rate of heat transfer through the wall will go up by UA for each degree rise in equivalent outdoor temperature due to solar radiation. Noting that the temperature rise due to solar radiation is

the rate of additional heat gain through the wall becomes

The total solar radiation incident on the entire wall is Q solar = A_sq· solar. Therefore, the fraction of incident solar heat transferred to the interior of the house is

Chapter: 5 Heat Gain from People, Lights, and Appliances

The conversion of chemical or electrical energy to thermal energy in a building constitutes the internal heat gain or internal load of a building. The primary sources of internal heat gain are people, lights, appliances, and miscellaneous equipment such as computers, printers, and copiers (Fig. 16–26). Internal heat gain is usually ignored in design heating load calculations to ensure that the heating system can do the job even when there is no heat gain, but it is always considered in design cooling load calculations since the internal heat gain usually constitutes a significant fraction of it.

People

The average amount of heat given off by a person depends on the level of activity, and can range from about 100 W for a resting person to more than 500 W for a physically very active person. Typical rates of heat dissipation by people are given in Table 8 for various activities in various application areas. Note that latent heat constitutes about one-third of the total heat dissipated during resting, but rises to almost two-thirds the level during heavy physical work. Also, about 30 percent of the sensible heat is lost by convection and the remaining 70 percent by radiation. The latent and convective sensible heat losses represent the “instant” cooling load for people since they need to be removed immediately. The radiative sensible heat, on the other hand, is first absorbed by the surrounding surfaces and then released gradually with some delay.

It is interesting to note that an average person dissipates latent heat at a minimum rate of 30 W while resting. Noting that the enthalpy of vaporization of water at 33°C is 2424 kJ/kg, the amount of water an average person loses a day by evaporation at the skin and the lungs is (Fig. 27) which justifies the sound advice that a person must drink at least 1 L of water every day. Therefore, a family of four will supply 4 L of water a day to the air in the house while just resting. This amount will be much higher during heavy work.

Heat given off by people usually constitutes a significant fraction of the sensible and latent heat gain of a building, and may dominate the cooling load in high occupancy buildings such as theaters and concert halls. The rate of heat gain from people given in Table 8 is quite accurate, but there is considerable uncertainty in the internal load due to people because of the difficulty in predicting the number of occupants in a building at any given time. The design cooling load of a building should be determined assuming full occupancy. In the absence of better data, the number of occupants can be estimated on the basis of one occupant per 1 m2 in auditoriums, 2.5 m2 in schools, 3–5 m2 in retail stores, and 10–15 m2 in offices.

Lights

Lighting constitutes about 7 percent of the total energy use in residential buildings and 25 percent in commercial buildings. Therefore, lighting can have a significant impact on the heating and cooling loads of a building. Not counting the candle light used for emergencies and romantic settings, and the kerosene lamps used during camping, all modern lighting equipment is powered by electricity. The basic types of electric lighting devices are incandescent, fluorescent, and gaseous discharge lamps.

The amount of heat given off per lux of lighting varies greatly with the type of lighting, and thus we need to know the type of lighting installed in order to predict the lighting internal heat load accurately. The lighting efficacy of common types of lighting is given in Table 9. Note that incandescent lights are the least efficient lighting sources, and thus they will impose the greatest load on cooling systems (Fig. 16–28). So it is no surprise that practically all office buildings use high-efficiency fluorescent lights despite their higher initial cost. Note that incandescent lights waste energy by (1) consuming more electricity for the same amount of lighting and (2) making the cooling system work harder and longer to remove the heat given off. Office spaces are usually well lit, and the lighting energy consumption in office buildings is about 20 to   30 W/m2 (2 to 3 W/ft2) of floor space.

The energy consumed by the lights is dissipated by convection and radiation. The convection component of the heat constitutes about 40 percent for fluorescent lamps, and it represents the instantaneous part of the cooling load due to lighting. The remaining part is in the form of radiation that is absorbed and reradiated by the walls, floors, ceiling, and the furniture, and thus they affect the cooling load with time delay. Therefore, lighting may continue contributing to the cooling load by reradiation even after the lights have been turned off. Sometimes it may be necessary to consider time lag effects when determining the design cooling load.

The ratio of the lighting wattage in use to the total wattage installed is called the usage factor, and it must be considered when determining the heat gain due to lighting at a given time since installed lighting does not give off heat unless it is on. For commercial applications such as supermarkets and shopping centers, the usage factor is taken to be unity.

Equipment and Appliances

Most equipment and appliances are driven by electric motors, and thus the heat given off by an appliance in steady operation is simply the power consumed by its motor. For a fan, for example, part of the power consumed by the motor is transmitted to the fan to drive it, while the rest is converted to heat because of the inefficiency of the motor. The fan transmits the energy to the air molecules and increases their kinetic energy. But this energy is also converted to heat as the fast-moving molecules are slowed down by other molecules and stopped as a result of friction. Therefore, we can say that the entire energy consumed by the motor of the fan in a room is eventually converted to heat in that room. Of course, if the motor is in one room (say, room A) and the fan is in another (say, room B), then the heat gain of room B will be equal to the power transmitted to the fan only, while the heat gain of room A will be the heat generated by the motor due to its inefficiency (Fig. 29).

The power rating W_motor on the label of a motor represents the power that the motor will supply under full load conditions. But a motor usually operates at part load, sometimes at as low as 30 to 40 percent, and thus it consumes and delivers much less power than the label indicates. This is characterized by the load factor f_load of the motor during operation, which is f_load = 1.0 for full load. Also, there is an inefficiency associated with the conversion of electrical energy to rotational mechanical energy. This is characterized by the motor efficiency h_motor, which decreases with decreasing load factor. Therefore, it is not a good idea to oversize the motor since oversized motors operate at a low load factor and thus at a lower efficiency. Another factor that affects the amount of heat generated by a motor is how long a motor actually operates. This is characterized by the usage factor f_usage, with f_usage = 1.0 for continuous operation. Motors with very low usage factors such as the motors of dock doors can be ignored in calculations. Then the heat gain due to a motor inside a conditioned space can be expressed as

Heat generated in conditioned spaces by electric, gas, and steam appliances such as a range, refrigerator, freezer, TV, dishwasher, clothes washer, drier, computers, printers, and copiers can be significant, and thus must be considered when determining the peak cooling load of a building. There is considerable uncertainty in the estimated heat gain from appliances owing to the variations in appliances and the varying usage schedules. The exhaust hoods in the kitchen complicate things further. Also, some office equipment such as printers and copiers consume considerable power in the standby mode. A 350-W laser printer, for example, may consume 175 W and a 600-W computer may consume 530 W when in standby mode.

The heat gain from office equipment in a typical office with computer terminals on most desks can be up to 47 W/m2. This value can be 10 times as large for computer rooms that house mainframe computers. When the equipment inventory of a building is known, the equipment heat gain can be determined more accurately using the data given in the ASHRAE Handbook of Fundamentals.

The presence of thermostatic controls and typical usage practices make it highly unlikely for all the appliances in a conditioned space to operate at full load. A more realistic approach is to take 50 percent of the total nameplate ratings of the appliances to represent the maximum use. Therefore, the peak heat gain from appliances is taken to be

regardless of the type of energy or fuel used. For cooling load estimate, about 34 percent of heat gain can be assumed to be latent heat, with the remaining 66 percent to be sensible in this case.

In hooded appliances, the air heated by convection and the moisture generated are removed by the hood. Therefore, the only heat gain from hooded appliances is radiation, which constitutes up to 32 percent of the energy consumed by the appliance (Fig. 30). Therefore, the design value of heat gain from hooded electric or steam appliances is simply half of this 32 percent.

Chapter: 6 Heat Transfer through Walls and Roofs

Under steady conditions, the rate of heat transfer through any section of a building wall or roof can be determined from

where T_i and T_o are the indoor and outdoor air temperatures, A_s is the heat transfer area, U is the overall heat transfer coefficient (the U-factor), and     R = 1/U is the overall unit thermal resistance (the R-value). Walls and roofs of buildings consist of various layers of materials, and the structure and operating conditions of the walls and the roofs may differ significantly from one building to another. Therefore, it is not practical to list the R-values (or U-factors) of different kinds of walls or roofs under different conditions. Instead, the overall R-value is determined from the thermal resistances of the individual components using the thermal resistance network. The overall thermal resistance of a structure can be determined most accurately in a lab by actually assembling the unit and testing it as a whole, but this approach is usually very time consuming and expensive. The analytical approach described here is fast and straightforward, and the results are usually in good agreement with the experimental values.

The unit thermal resistance of a plane layer of thickness L and thermal conductivity k can be determined from R = L/k. The thermal conductivity and other properties of common building materials are given in the appendix. The unit thermal resistances of various components used in building structures are listed in Table 10 for convenience.

Heat transfer through a wall or roof section is also affected by the convection and radiation heat transfer coefficients at the exposed surfaces. The effects of convection and radiation on the inner and outer surfaces of walls and roofs are usually combined into the combined convection and radiation heat transfer coefficients (also called surface conductances) h_i and h_o, respectively, whose values are given in Table 11 for ordinary surfaces (e = 0.9) and reflective surfaces (e = 0.2 or 0.05). Note that surfaces having a low emittance also have a low surface conductance due to the reduction in radiation heat transfer. The values in the table are based on a surface temperature of 21°C (72°F) and a surface–air temperature difference of 5.5°C (10°F). Also, the equivalent surface temperature of the environment is assumed to be equal to the ambient air temperature. Despite the convenience it offers, this assumption is not quite accurate because of the additional radiation heat loss from the surface to the clear sky. The effect of sky radiation can be accounted for approximately by taking the outside temperature to be the average of the outdoor air and sky temperatures.

The inner surface heat transfer coefficient h_i remains fairly constant through-out the year, but the value of h_o varies considerably because of its dependence on the orientation and wind speed, which can vary from less than 1 km/h in calm weather to over 40 km/h during storms. The commonly used values of h_i and h_o for peak load calculations are

which correspond to design wind conditions of 24 km/h (15 mph) for winter and 12 km/h (7.5 mph) for summer. The corresponding surface thermal resistances (R-values) are determined from R_i = l/h_i and R_o = l/h_o. The surface conductance values under still air conditions can be used for interior surfaces as well as exterior surfaces in calm weather.

Building components often involve trapped air spaces between various layers. Thermal resistances of such air spaces depend on the thickness of the  layer, the temperature difference across the layer, the mean air temperature, the emissivity of each surface, the orientation of the air layer, and the direction of heat transfer. The emissivities of surfaces commonly encountered in buildings are given in Table 12. The effective emissivity of a plane-parallel air space is given by

where e₁ and e₂ are the emissivities of the surfaces of the air space.  Table 12 also lists the effective emissivities of air spaces for the cases where (1) the emissivity of one surface of the air space is e while the emissivity of the other surface is 0.9 (a building material) and (2) the emissivity of both surfaces is e. Note that the effective emissivity of an air space between building materials is 0.82/0.03 = 27 times that of an air space between surfaces covered with aluminum foil. For specified surface temperatures, radiation heat transfer through an air space is proportional to effective emissivity, and thus the rate of radiation heat transfer in the ordinary surface case is 27 times that of the reflective surface case.

Table 13 lists the thermal resistances of 20-mm-, 40-mm-, and 90-mm- (0.75-in, 1.5-in, and 3.5-in) thick air spaces under various conditions.

The thermal resistance values in the table are applicable to air spaces of uniform thickness bounded by plane, smooth, parallel surfaces with no air leakage. Thermal resistances for other temperatures, emissivities, and air spaces can be obtained by interpolation and moderate extrapolation. Note that the presence of a low-emissivity surface reduces radiation heat transfer across an air space and thus significantly increases the thermal resistance. The thermal effectiveness of a low-emissivity surface will decline, however, if the condition of the surface changes as a result of some effects such as condensation, surface oxidation, and dust accumulation.

The R-value of a wall or roof structure that involves layers of uniform thickness is determined easily by simply adding up the unit thermal resistances of the layers that are in series. But when a structure involves components such as wood studs and metal connectors, then the thermal resistance network involves parallel connections and possible two-dimensional effects. The overall R-value in this case can be determined by assuming (1) parallel heat flow paths through areas of different construction or (2) isothermal planes normal to the direction of heat transfer. The first approach usually over-predicts the overall thermal resistance, whereas the second approach usually underpredicts it. The parallel heat flow path approach is more suitable for wood frame walls and roofs, whereas the isothermal planes approach is more suitable for masonry or metal frame walls.

The thermal contact resistance between different components of building structures ranges between 0.01 and 0.1 m2 · °C/W, which is negligible in most cases. However, it may be significant for metal building components such as steel framing members.

The construction of wood frame flat ceilings typically involve 2-in X 6-in joists on 400-mm (16-in) or 600-mm (24-in) centers. The fraction of framing is usually taken to be 0.10 for joists on 400-mm centers and 0.07 for joists on 600-mm centers.

Most buildings have a combination of a ceiling and a roof with an attic space in between, and the determination of the R-value of the roof–attic–ceiling combination depends on whether the attic is vented or not. For adequately ventilated attics, the attic air temperature is practically the same as the outdoor air temperature, and  thus  heat  transfer  through  the  roof  is  governed  by  the R-value of the ceiling only. However, heat is also transferred between the roof and the ceiling by radiation, and it needs to be considered (Fig. 33). The major function of the roof in this case is to serve as a radiation shield by blocking off solar radiation. Effectively ventilating the attic in summer should not lead one to believe that heat gain to the building through the attic is greatly reduced. This is because most of the heat transfer through the attic is by radiation.

Radiation heat transfer between the ceiling and the roof can be  minimized by covering at least one side of the attic (the roof or the ceiling side) by a reflective material, called radiant barrier, such as aluminum foil or aluminum coated paper. Tests on houses with R-19 attic floor insulation have shown that radiant barriers can reduce summer ceiling heat gains by 16 to 42 percent compared to an attic with the same insulation level and no radiant barrier. Considering that the ceiling heat gain represents about 15 to 25 percent of the total cooling load of a house, radiant barriers will reduce the air conditioning costs by 2 to 10 percent. Radiant barriers also reduce the heat loss in winter through the ceiling, but tests have shown that the percentage reduction in heat losses is less. As a result, the percentage reduction in heating costs will be less than the reduction in the air-conditioning costs. Also, the values given are for new and undusted radiant barrier installations, and percentages will be lower for aged or dusty radiant barriers.

Some possible locations for attic radiant barriers are given in Fig. 34. In whole house tests on houses with R-19 attic floor insulation, radiant barriers have reduced the ceiling heat gain by an average of 35 percent when the radiant barrier is installed on the attic floor, and by 24 percent when it is attached to the bottom of roof rafters. Test cell tests also demonstrated that the best location for radiant barriers is the attic floor, provided that the attic is not used as a storage area and is kept clean.

For unvented attics, any heat transfer must occur through (1) the ceiling, (2) the attic space, and (3) the roof (Fig. 35). Therefore, the overall R-value of the roof–ceiling combination with an unvented attic depends on the combined effects of the R-value of the ceiling and the R-value of the roof as well as the thermal resistance of the attic space. The attic space can be treated as an air layer in the analysis. But a more practical way of accounting for its effect is to consider surface resistances on the roof and ceiling surfaces facing each other. In this case, the R-values of the ceiling and the roof are first determined separately (by using convection resistances for the still-air case for the attic surfaces). Then it can be shown that the overall R-value of the ceiling- roof combination per unit area of the ceiling can be expressed as

where Aceiling and Aroof are the ceiling and roof areas, respectively. The area ratio is equal to 1 for flat roofs and is less than 1 for pitched roofs. For a 45 pitched roof, the area ratio is A_ceiling/A_roof =
1/ = 0.707. Note that the pitched roof has a greater  area for heat transfer than the flat ceiling, and the area ratio accounts for the reduction in the unit R-value of the roof when expressed per unit area of the ceiling. Also, the direction of heat flow is up in winter (heat loss through the roof) and down in summer (heat gain through the roof).

The R-value of a structure determined by analysis assumes that the materials used and the quality of workmanship meet the standards. Poor workmanship and substandard materials used during construction may result in R-values that deviate from predicted values. Therefore, some engineers use a safety factor in their designs based on experience in critical applications.

Chapter: 7 Heat Loss from Basement Walls and Floors

The floors and the underground portion of the walls of a basement are in direct contact with the ground, which is usually at a different temperature than the basement, and thus there is heat transfer between the basement and the ground. This is conduction heat transfer because of the direct contact between the walls and the floor, and it depends on the temperature difference between the basement and the ground, the construction of the walls and the floor, and the thermal conductivity of the surrounding earth. There is considerable uncertainty in the ground heat loss calculations, and they probably constitute the least accurate part of heat load estimates of a building because of the large thermal mass of the ground and the large variation of the thermal conductivity of the soil [it varies between 0.5 and 2.5 W/m · C (or 0.3 to 1.4 Btu/h · ft · F), depending on the composition and moisture content]. However, ground heat losses are a small fraction of total heat load of a large building, and thus it has little effect on the overall heat load.

Temperature measurements of uninsulated basements indicate that heat conduction through the ground is not one-dimensional, and thus it cannot be estimated by a simple one-dimensional heat conduction analysis. Instead, heat conduction is observed to be two-dimensional with nearly circular concentric heat flow lines centered at the intersection of the wall and the earth (Fig. 36). When partial insulation is applied to the walls, the heat flow lines tend to be straight lines rather than being circular. Also, a basement wall whose top portion is exposed to ambient air may act as a thermal bridge, conducting heat upward and dissipating it to the ambient from its top part. This vertical heat flow may be significant in some cases.

Despite its complexity, heat loss through the below-grade section of basement walls can be determined easily from

The overall heat transfer coefficients at different  depths  are  given  in  Table 14a for depth increments of 0.3 m (or 1 ft) for uninsulated and insulated concrete walls. These values are based on a soil thermal conductivity of 1.38 W/m · °C (0.8 Btu/h · ft · °F). Note that the heat transfer coefficient values decrease with increasing depth since the heat at a lower section must pass through a longer path to reach the ground surface. For a specified wall, U_{wall, avg} is simply the arithmetic average of the U_wall values corresponding to the different sections of the wall. Also note that heat loss through a depth increment is equal to the U_wall value of the increment multiplied by the perimeter of the building, the depth increment, and the temperature difference.

The interior air temperature of the basement can vary considerably, depending on whether it is being heated or not. In the absence of reliable data, the basement temperature can be taken to be 10°C since the heating system, water heater, and heating ducts are often located in the basement. Also, the ground surface temperature fluctuates about the mean winter ambient temperature by an amplitude A that varies with geographic location and the condition of the surface, as shown in Fig. 37. Therefore, a reasonable value for the design temperature of ground surface can be obtained by subtracting A for the specified location from the mean winter air temperature. That is,

Heat loss through the basement floor is much smaller since the heat flow path to the ground surface is much longer in this case. It is calculated in a similar manner from

where U_floor is the overall heat transfer coefficient at the basement floor whose values are listed in Table 14b, A_floor is the floor area, and the temperature difference is the same as the one used for the basement wall.

The temperature of an unheated below-grade basement is between the temperatures of the rooms above and the ground temperature. Heat losses from the water heater and the space heater located in the basement usually keep the air near the basement ceiling sufficiently warm. Heat losses from the rooms above to the basement can be neglected in such cases. This will not be the case, however, if the basement has windows.

Concrete Floors on Grade (at Ground Level)

Many residential and commercial buildings do not have a basement, and the floor sits directly on the ground at or slightly above the ground level. Research indicates that heat loss from such floors is mostly through the perimeter to the outside air rather than through the floor into the ground, as shown in  Fig. 39. Therefore, total heat loss from a concrete slab floor is proportional to the perimeter of the slab instead of the area of the floor and is expressed as

where U_grade represents the rate of heat transfer from the slab per unit temperature difference between the indoor temperature T_indoor and the outdoor tem- perature T_outdoor and per unit length of the perimeter p_floor of the building.

Typical values of U_grade are listed in Table 14c for four common types of slab-on-grade construction for mild, moderate, and severe weather conditions. The ground temperature is not involved in the formulation since the slab is located above the ground level and heat loss to the ground is negligible. Note from the table that perimeter insulation of slab-on-grade reduces heat losses considerably, and thus it saves energy while enhancing comfort. Insulation is a must for radiating floors that contain heated pipes or ducts through which hot water or air is circulated since heat loss in the uninsulated case is about three times that of the insulated case. This is also the case when base board heaters are used on the floor near the exterior walls. Heat transfer through the floors and the basement is usually ignored in cooling load calculations.

Heat Loss from Crawl Spaces

A crawl space can be considered to be a small basement except that it may be vented year round to prevent the accumulation of moisture and radioactive gases such as radon. Venting the crawl space during the heating season creates a low temperature region underneath the house and causes considerable heat loss through the floor. The ceiling of the crawl space (i.e., the floor of the building) in such cases must be insulated. If the vents are closed during the heating season, then the walls of the crawl space can be insulated instead.

The temperature of the crawl space will be very close to the ambient air temperature when it is well ventilated. The heating ducts and hot water pipes passing through the crawl space must be adequately insulated in this case. In severe climates, it may even be necessary to insulate the cold water pipes to prevent freezing. The temperature of the crawl space will approach the indoor temperature when the vents are closed for the heating season. The air infiltration in this case is estimated to be 0.67 air change per hour.

When the crawl space temperature is known, heat loss through the floor of the building is determined from

where U_{building floor} is the overall heat transfer coefficient for the floor, A_floor is the floor area, and T_indoor and T_crawl are the indoor and crawl space temperatures, respectively.

Overall heat transfer coefficients associated with the walls, floors, and ceilings of typical crawl spaces are given in Table 15. Note that heat loss  through the uninsulated floor to the crawl space is three times that of the insulated floor. The ground temperature can be taken to be 10°C when calculating heat loss from the crawl space to the ground. Also, the infiltration heat loss from the crawl space can be determined from

where ACH is the air changes per hour, V_crawl is the volume of the crawl space, and T_crawl and T_ambient are the crawl space and ambient temperatures, respectively.

In the case of closed vents, the steady state temperature of the crawl space will be between the indoors and outdoors temperatures and can be determined from the energy balance expressed as

and assuming all heat transfer to be toward the crawl space for convenience in formulation.

Chapter: 8 Heat Transfer through Windows

Windows are glazed apertures in the building envelope that typically consist of single or multiple glazing (glass or plastic), framing, and shading. In a building envelope, windows offer the least resistance to heat transfer. In a typical-house, about one-third of the total heat loss in winter occurs through the windows. Also, most air infiltration occurs at the edges of the windows. The solar heat gain through the windows is responsible for much of the cooling load in summer. The net effect of a window on the heat balance of a building depends on the characteristics and orientation of the window as well as the solar and weather data. Workmanship is very important in the construction and installation of windows to provide effective sealing around the edges while allowing them to be opened and closed easily.

Despite being so undesirable from an energy conservation point of view, windows are an essential part of any building envelope since they enhance the appearance of the building, allow daylight and solar heat to come in, and allow people to view and observe outside without leaving their home. For low-rise buildings, windows also provide easy exit areas during emergencies such as fire. Important considerations in the selection of windows are thermal comfort and energy conservation. A window should have a good light transmittance while providing effective resistance to heat transfer. The lighting requirements of a building can be minimized by maximizing the use of natural daylight. Heat loss in winter through the windows can be minimized by using airtight double- or triple-pane windows with spectrally selective films or coatings, and letting in as much solar radiation as possible. Heat gain and thus cooling load in summer can be minimized by using effective internal or external shading on the windows.

Even in the absence of solar radiation and air infiltration, heat transfer through the windows is more complicated than it appears to be. This is be- cause the structure and properties of the frame are quite different than the glazing. As a result, heat transfer through the frame and the edge section of the glazing adjacent to the frame is two-dimensional. Therefore, it is customary to consider the window in three regions when analyzing heat transfer through it: (1) the center-of-glass, (2) the edge-of-glass, and (3) the frame regions, as shown in Fig. 41. Then the total rate of heat transfer through the window is determined by adding the heat transfer through each region as

is the U-factor or the overall heat transfer coefficient of the window; A_window is the window area; A_center, A_edge, and A_frame are the areas of the center, edge, and frame sections of the window, respectively; and U_center, U_edge, and U_frame are the heat transfer coefficients for the center, edge, and frame sections of the window. Note that A_window = A_center + A_edge + A_frame, and the overall U– factor of the window is determined from the area-weighed U-factors of each region of the window. Also, the inverse of the U-factor is the R-value, which is the unit thermal resistance of the window (thermal resistance for a unit area). Consider steady one-dimensional heat transfer through a single-pane glass of thickness L and thermal conductivity k. The thermal resistance network of this problem consists of surface resistances on the inner and outer surfaces and the conduction resistance of the glass in series, as shown in Fig. 42, and the total resistance on a unit area basis can be expressed as

Using common values of 3 mm for the thickness and 0.92 W/m · °C for the thermal conductivity of the glass and the winter design values of 8.29 and 34.0 W/m2 · °C for the inner and outer surface heat transfer coefficients, the thermal resistance of the glass is determined to be

That is, the glass layer itself contributes about 2 percent of the total thermal resistance of the window, which is negligible. The situation would not be much different if we used acrylic, whose thermal conductivity is 0.19 W/m · °C, in- stead of glass. Therefore, we cannot reduce the heat transfer through the window effectively by simply increasing the thickness of the glass. But we can reduce it by trapping still air between two layers of glass. The result is a double-pane window, which has become the norm in window construction. The thermal conductivity of air at room temperature is k_air = 0.025 W/m · °C, which is one-thirtieth that of glass. Therefore, the thermal resistance of 1-cm-thick still air is equivalent to the thermal resistance of a 30-cm-thick glass layer. Disregarding the thermal resistances of glass layers, the thermal resistance and U-factor of a double-pane window can be expressed as (Fig. 43)

where h_space = h_{rad, space} + h_{conv, space} is the combined radiation and convection heat transfer coefficient of the space trapped between the two glass layers.

Roughly half of the heat transfer through the air space of a double-pane window is by radiation and the other half is by conduction (or convection, if there is any air motion). Therefore, there are two ways to minimize h_space and thus the rate of heat transfer through a double-pane window:

• Minimize radiation heat transfer through the air space. This can be done by reducing the emissivity of glass surfaces by coating them with low-emissivity (or “low-e” for short) material. Recall that the effective emissivity of two parallel plates of emissivities e₁ and e₂ is given by

The emissivity of an ordinary glass surface is 0.84. Therefore, the effective emissivity of two parallel glass surfaces facing each other is 0.72. But when the glass surfaces are coated with a film that has an emissivity of 0.1, the effective emissivity reduces to 0.05, which is one-fourteenth of 0.72. Then for the same surface temperatures, radiation heat transfer will also go down by a factor of 14. Even if only one of the surfaces is coated, the overall emissivity reduces to 0.1, which is the emissivity of the coating. Thus it is no surprise that about one-fourth of all windows sold for residences have a low-e coating. The heat transfer coefficient hspace for the air space trapped between the two vertical parallel glass layers is given in Table 16 for 13-mm- ( -in) and 6-mm- ( -in) thick air spaces for various effective emissivities and temperature differences.

It can be shown that coating just one of the two parallel surfaces facing each other by a material of emissivity e reduces the effective emissivity nearly to e. Therefore, it is usually more economical to coat only one of the facing surfaces. Note from Fig. 44 that coating one of the interior surfaces of a doublepane window with a material having an emissivity of 0.1 reduces the rate of
heat transfer through the center section of the window by half.

• Minimize conduction heat transfer through air space. This can be done by increasing the distance d between the two glasses. However, this cannot be done indefinitely since increasing the spacing beyond a critical value initiates convection currents in the enclosed air space, which increases the heat transfer coefficient and thus defeats the purpose. Besides, increasing the spacing also increases the thickness of the necessary framing and the cost of the window.

Experimental studies have shown that when the spacing d is less than about 13 mm, there is no convection, and heat transfer through the air is by conduction. But as the spacing is increased further, convection currents appear in the air space, and the increase in heat transfer coefficient offsets any benefit obtained by the thicker air layer. As a result, the heat transfer coefficient remains nearly constant, as shown in Fig. 16–44. Therefore, it makes no sense to use an air space thicker than 13 mm in a double-pane window unless a thin polyester film is used to divide the air space into two halves to suppress convection currents. The film provides added insulation without adding much to the weight or cost of the double-pane window. The thermal resistance of the window can be increased further by using triple- or quadruple-pane windows whenever it is economical to do so. Note that using a triple-pane window instead of a double-pane reduces the rate of heat transfer through the center section of the window by about one-third.

Another way of reducing conduction heat transfer through a double-pane window is to use a less-conducting fluid such as argon or krypton to fill the gap between the glasses instead of air. The gap in this case needs to be well sealed to prevent the gas from leaking outside. Of course, another alternative is to evacuate the gap between the glasses completely, but it is not practical to do so.

Edge-of-Glass U-Factor of a Window

The glasses in double- and triple-pane windows are kept apart from each other at a uniform distance by spacers made of metals or insulators like aluminum, fiberglass, wood, and butyl. Continuous spacer strips are placed around the glass perimeter to provide edge seal as well as uniform spacing. However, the spacers also serve as undesirable “thermal bridges” between the glasses, which are at different temperatures, and this short-circuiting may increase heat transfer through the window considerably. Heat transfer in the edge region of a window is two-dimensional, and lab measurements indicate that the edge ef- fects are limited to a 6.5-cm-wide band around the perimeter of the glass.

The U-factor for the edge region of a window is given in Fig. 16–45 relative to the U-factor for the center region of the window. The curve would be a straight diagonal line if the two U-values were equal to each other. Note that this is almost the case for insulating spacers such as wood and fiberglass. But the U-factor for the edge region can be twice that of the center region for con- ducting spacers such as those made of aluminum. Values for steel spacers fall between the two curves for metallic and insulating spacers. The edge effect is not applicable to single-pane windows.

Frame U-Factor

The framing of a window consists of the entire window except the glazing. Heat transfer through the framing is difficult to determine because of the different window configurations, different sizes, different constructions, and different combination of materials used in the frame construction. The type of glazing such as single pane, double pane, and triple pane affects the thickness of the framing and thus heat transfer through the frame. Most frames are made of wood, aluminum, vinyl, or fiberglass. However, using a combination of these materials (such as aluminum-clad wood and vinyl-clad aluminum) is also common to improve appearance and durability.

Aluminum is a popular framing material because it is inexpensive, durable, and easy to manufacture, and does not rot or absorb water like wood. However, from a heat transfer point of view, it is the least desirable framing material because of its high thermal conductivity. It will come as no surprise that the U-factor of solid aluminum frames is the highest, and thus a window with aluminum framing will lose much more heat than a comparable window with wood or vinyl framing. Heat transfer through the aluminum framing members can be reduced by using plastic inserts between components to serve as thermal barriers. The thickness of these inserts greatly affects heat transfer through the frame. For aluminum frames without the plastic strips, the primary resistance to heat transfer is due to the interior surface heat transfer co- efficient. The U-factors for various frames are listed in Table 17 as a function of spacer materials and the glazing unit thicknesses. Note that the U-factor of metal framing and thus the rate of heat transfer through a metal window frame is more than three times that of a wood or vinyl window frame.

Interior and Exterior Surface Heat Transfer Coefficients

Heat transfer through a window is also affected by the convection and radiation heat transfer coefficients between the glass surfaces and surroundings. The effects of convection and radiation on the inner and outer surfaces of glazings are usually combined into the combined convection and radiation heat transfer coefficients h_i and h_o, respectively. Under still air conditions, the combined heat transfer coefficient at the inner surface of a vertical window can be determined from

where T_g = glass temperature  in  K,  T_i = indoor  air  temperature  in  K,  e_g = emissivity of the inner surface of the glass exposed to the room (taken to  be  0.84  for  uncoated  glass),  and  s = 5.67 X 10-8   W/m2   ·  K4   is  the Stefan–Boltzmann constant. Here the temperature of the interior surfaces facing the window is assumed to be equal to the indoor air temperature. This assumption is reasonable when the window faces mostly interior walls, but  it becomes questionable when the window is exposed to heated or cooled surfaces or to other windows. The commonly used value of h_i for peak load calculation is

which corresponds to the winter design conditions of T_i = 22°C and T_g = -7°C for uncoated glass with e_g = 0.84. But the same value of h_i can also be used for summer design conditions as it corresponds to summer con- ditions of T_i = 24°C and T_g = 32°C. The values of h_i for various temperatures and glass emissivities are given in Table 18. The commonly used values of h_o for peak load calculations are the same as those used for outer wall surfaces (34.0 W/m2 · °C for winter and 22.7 W/m2 · °C for summer).

Overall U-Factor of Windows

The overall U-factors for various kinds of windows and skylights are evaluated using computer simulations and laboratory testing for winter design conditions; representative values are given in Table 19. Test data may provide more accurate information for specific products and should be preferred when available. However, the values listed in the table can be used to obtain satisfactory results under various conditions in the absence of product-specific data. The U-factor of a fenestration product that differs considerably from the ones in the table can be determined by (1) determining the fractions      of the area that are frame, center-of-glass, and edge-of-glass (assuming a 65-mm-wide band around the perimeter of each glazing), (2) determining the U-factors for each section (the center-of-glass and edge-of-glass U-factors can be taken from the first two columns of Table 19 and the frame U-factor can be taken from Table 18 or other sources), and (3) multiplying the area fractions and the U-factors for each section and adding them up (or from   Eq. 16–34 for U_window).

Glazed wall systems can be treated as fixed windows. Also, the data for double-door windows can be used for single-glass doors. Several observations can be made from the data in the table:

1. Skylight U-factors are considerably greater than those of vertical windows. This is because the skylight area, including the curb, can be 13 to 240 percent greater than the rough opening area. The slope of the skylight also has some effect.
   
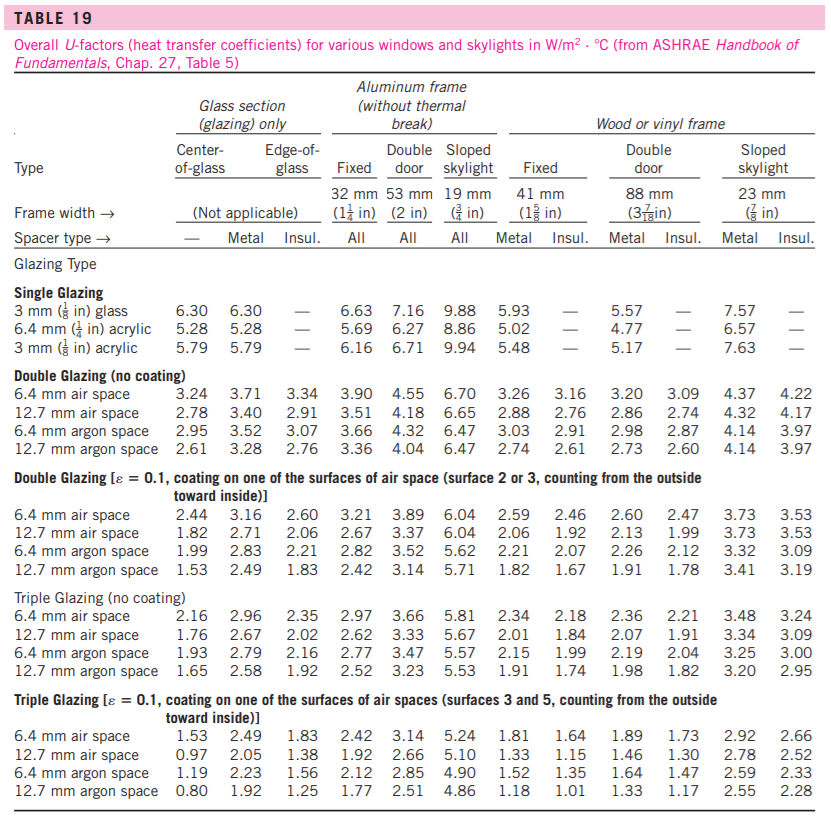
2. The U-factor of multiple-glazed units can be reduced considerably by filling cavities with argon gas instead of dry air. The performance of CO₂-filled units is similar to those filled with argon. The U-factor can be reduced even further by filling the glazing cavities with krypton gas.
3. Coating the glazing surfaces with low-e (low-emissivity) films reduces the U-factor significantly. For multiple-glazed units, it is adequate to coat one of the two surfaces facing each other.
4. The thicker the air space in multiple-glazed units, the lower the U-factor, for a thickness of up to 13 mm (¹ in) of air space. For a specified number of glazings, the window with thicker air layers will have a lower U-factor. For a specified overall thickness of glazing, the higher the number of glazings, the lower the U-factor. Therefore, a triple-pane window with air spaces of 6.4 mm (two such air spaces) will have a lower U-value than a double-pane window with an air space of 12.7 mm.
5. Wood or vinyl frame windows have a considerably lower U-value than comparable metal-frame windows. Therefore, wood or vinyl frame windows are called for in energy-efficient designs.

Chapter: 9 Solar Heat Gain through Windows

The sun is the primary heat source of the earth, and the solar irradiance on a surface normal to the sun’s rays beyond the earth’s atmosphere at the mean earth–sun distance of 149.5 million km is called the solar constant. The accepted value of the solar constant is 1373 W/m2 (435.4 Btu/h · ft2), but its value changes by 3.5 percent from a maximum of 1418 W/m2 on January 3 when the earth is farthest away from the sun, to a minimum of 1325 W/m2 on July 4 when the earth is closest to the sun. The spectral distribution of solar radiation beyond the earth’s atmosphere resembles the energy emitted by a blackbody at 5782°C, with about 9 percent of the energy contained in the ultraviolet region (at wavelengths between 0.29 to 0.4 µ,m), 39 percent in the visible region (0.4 to 0.7 µ,m), and the remaining 52 percent in the near- infrared region (0.7 to 3.5 µ,m). The peak radiation occurs at a wavelength of about 0.48 µ,m, which corresponds to the green color portion of the visible spectrum. Obviously a glazing material that transmits the visible part of the spectrum while absorbing the infrared portion is ideally suited for an application that calls for maximum daylight and minimum solar heat gain. Surprisingly, the ordinary window glass approximates this behavior remarkably well (Fig. 49).

Part of the solar radiation entering the earth’s atmosphere is scattered and absorbed by air and water vapor molecules, dust particles, and water droplets in the clouds, and thus the solar radiation incident on earth’s surface is less than the solar constant. The extent of the attenuation of solar radiation depends on the length of the path of the rays through the atmosphere as well as the composition of the atmosphere (the clouds, dust, humidity, and smog) along the path. Most ultraviolet radiation is absorbed by the ozone in the upper atmosphere. At a solar altitude of 41.8°, the total energy of direct solar radiation incident at sea level on a clear day consists of about 3 percent ultra- violet, 38 percent visible, and 59 percent infrared radiation.

The part of solar radiation that reaches the earth’s surface without being scattered or absorbed is the direct radiation. Solar radiation that is scattered or re-emitted by the constituents of the atmosphere is the diffuse radiation. Direct radiation comes directly from the sun following a straight path, whereas diffuse radiation comes from all directions in the sky. The entire radiation reaching the ground on an overcast day is diffuse radiation. The radiation reaching a surface, in general, consists of three components: direct radiation, diffuse radiation, and radiation reflected onto the surface from surrounding surfaces (Fig. 50). Common surfaces such as grass, trees, rocks, and concrete reflect about 20 percent of the radiation while absorbing the rest. Snow-covered surfaces, however, reflect 70 percent of the incident radiation. Radiation incident on a surface that does not have a direct view of the sun consists of diffuse and reflected radiation. Therefore, at solar noon, solar radiations incident on the east, west, and north surfaces of a south-facing house are identical since they all consist of diffuse and reflected components. The difference between the radiations incident on the south and north walls in this case gives the magnitude of direct radiation incident on the south wall.

When solar radiation strikes a glass surface, part of it (about 8 percent for uncoated clear glass) is reflected back to outdoors, part of it (5 to 50 percent, depending on composition and thickness) is absorbed within the glass, and the remainder is transmitted indoors, as shown in Fig. 51. The conservation of energy principle requires that the sum of the transmitted, reflected, and absorbed solar radiations be equal to the incident solar radiation. That is,

where t_s is the transmissivity, r_s is the reflectivity, and a_s is the absorptivity of the glass for solar energy, which are the fractions of incident solar radiation transmitted, reflected, and absorbed, respectively. The standard 3-mm- (¹-in) thick single-pane double-strength clear window glass transmits 86 percent, reflects 8 percent, and absorbs 6 percent of the solar energy incident on it. The radiation properties of materials are usually given for normal incidence, but can also be used for radiation incident at other angles since the transmissivity, reflectivity, and absorptivity of the glazing materials remain essentially constant for incidence angles up to about 60° from the normal.

The hourly variation of solar radiation incident on the walls and windows of a house is given in Table 20. Solar radiation that is transmitted indoors is partially absorbed and partially reflected each time it strikes a surface, but all of it is eventually absorbed as sensible heat by the furniture, walls, people, and so forth. Therefore, the solar energy transmitted inside a building represents a heat gain for the building. Also, the solar radiation absorbed by the glass is subsequently transferred to the indoors and outdoors by convection and radiation. The sum of the transmitted solar radiation and the portion of the absorbed radiation that flows indoors constitutes the solar heat gain of the building.

The fraction of incident solar radiation that enters through the glazing is called the solar heat gain coefficient SHGC and is expressed as

the absorbed and re-emitted (f_ia_s) portions of solar radiation incident on the window. The value of SHGC ranges from 0 to 1, with 1 corresponding to an opening in the wall (or the ceiling) with no glazing. When the SHGC of a window is known, the total solar heat gain through that window is determined from

where A_glazing is the glazing area of the window and q# solar, incident is the solar heat flux incident on the outer surface of the window, in W/m2.

Another way of characterizing the solar transmission characteristics of different kinds of glazing and shading devices is to compare them to a well known glazing material that can serve as a base case. This is done by taking the standard 3-mm- (¹-in) thick double-strength clear window glass sheet whose SHGC is 0.87 as the reference glazing and defining a shading coefficient SC as

Therefore, the shading coefficient of a single-pane clear glass window is SC = 1.0. The shading coefficients of other commonly used fenestration products are given in Table 21 for summer design conditions. The values for winter design conditions may be slightly lower because of the higher heat transfer coefficients on the outer surface due to high winds and thus higher rate of outward flow of solar heat absorbed by the glazing, but the difference is small.

Note that the larger the shading coefficient, the smaller the shading effect, and thus the larger the amount of solar heat gain. A glazing material with a large shading coefficient allows a large fraction of solar radiation to come in.

Shading devices are classified as internal shading and external shading, depending on whether the shading device is placed inside or outside. External shading devices are more effective in reducing the solar heat gain since they intercept the sun’s rays before they reach the glazing. The solar heat gain through a window can be reduced by as much as 80 percent by exterior shading. Roof overhangs have long been used for exterior shading of windows. The sun is high in the horizon in summer and low in winter. A properly sized roof overhang or a horizontal projection blocks off the sun’s rays completely in summer while letting in most of them in winter, as shown in Fig. 16–52. Such shading structures can reduce the solar heat gain on the south, southeast, and southwest windows in the northern hemisphere considerably. A window can also be shaded from outside by vertical or horizontal or architectural projections, insect or shading screens, and sun screens. To be effective, air must be able to move freely around the exterior device to carry away the heat absorbed by the shading and the glazing materials.

Some type of internal shading is used in most windows to provide privacy and aesthetic effects as well as some control over solar heat gain. Internal shading devices reduce solar heat gain by reflecting transmitted solar radiation back through the glazing before it can be absorbed and converted into heat in the building.

Draperies reduce the annual heating and cooling loads of a building by 5 to 20 percent, depending on the type and the user habits. In summer, they reduce heat gain primarily by reflecting back direct solar radiation (Fig. 53). The semiclosed air space formed by the draperies serves as an additional barrier against heat transfer, resulting in a lower U-factor for the window and thus a lower rate of heat transfer in summer and winter. The solar optical properties of draperies can be measured accurately, or they can be obtained directly from the manufacturers. The shading coefficient of draperies depends on the openness factor, which is the ratio of the open area between the fibers that permits the sun’s rays to pass freely, to the total area of the fabric. Tightly woven fabrics allow little direct radiation to pass through, and thus they have a small openness factor. The reflectance of the surface of the drapery facing the glazing has a major effect on the amount of solar heat gain. Light-colored draperies made of closed or tightly woven fabrics maximize the back reflection and thus minimize the solar gain. Dark-colored draperies made of open or semi-open woven fabrics, on the other hand, minimize the back reflection and thus maximize the solar gain.

The shading coefficients of drapes also depend on the way they are hung. Usually, the width of drapery used is twice the width of the draped area to allow folding of the drapes and to give them their characteristic “full” or “wavy” appearance. A flat drape behaves like an ordinary window shade. A flat drape has a higher reflectance and thus a lower shading coefficient than a full drape.

External shading devices such as overhangs and tinted glazings do not require operation, and provide reliable service over a long time without significant degradation during their service life. Their operation does not depend on a person or an automated system, and these passive shading devices are considered fully effective when determining the peak cooling load and the annual energy use. The effectiveness of manually operated shading devices, on the other hand, varies greatly depending on the user habits, and this variation should be considered when evaluating performance.

The primary function of an indoor shading device is to provide thermal comfort for the occupants. An unshaded window glass allows most of the incident solar radiation in, and also dissipates part of the solar energy it absorbs by emitting infrared radiation to the room. The emitted radiation and the transmitted direct sunlight may bother the occupants near the window. In winter, the temperature of the glass is lower than the room air temperature, causing excessive heat loss by radiation from the occupants. A shading device allows the control of direct solar and infrared radiation while providing various degrees of privacy and outward vision. The shading device is also at a higher temperature than the glass in winter, and thus reduces radiation loss from occupants. Glare from draperies can be minimized by using off-white colors.

Indoor shading devices, especially draperies made of a closed-weave fabric, are effective in reducing sounds that originate in the room, but they are not as effective against the sounds coming from outside.

The type of climate in an area usually dictates the type of windows to be used in buildings. In cold climates where the heating load is much larger than the cooling load, the windows should have the highest transmissivity for the entire solar spectrum, and a high reflectivity (or low emissivity) for the far infrared radiation emitted by the walls and furnishings of the room. Low-e windows are well suited for such heating-dominated buildings. Properly designed and operated windows allow more heat into the building over a heating season than it loses, making them energy contributors rather then energy losers. In warm climates where the cooling load is much larger than the heating load, the  windows should allow the visible solar radiation (light) in, but should block off the infrared solar radiation. Such windows can reduce the solar heat gain by 60 percent with no appreciable loss in daylighting. This behavior is approximated by window glazings that are coated with a heat-absorbing film outside and a low-e film inside (Fig. 54). Properly selected windows can reduce the cooling load by 15 to 30 percent compared to windows with clear glass.

Note that radiation heat transfer between a room and its windows is propor- tional to the emissivity of the glass surface facing the room, e_glass, and can be expressed as

Therefore, a low-e interior glass will reduce the heat loss by radiation in winter (T_glass < T_room) and heat gain by radiation in summer (T_glass > T_room).

Tinted glass and glass coated with reflective films reduce solar heat gain in summer and heat loss in winter. The conductive heat gains or losses can be minimized by using multiple-pane windows. Double-pane windows are usu- ally called for in climates where the winter design temperature is less than 7°C (45°F). Double-pane windows with tinted or reflective films are commonly used in buildings with large window areas. Clear glass is preferred for show- rooms since it affords maximum visibility from outside, but bronze-, gray-, and green-colored glass are preferred in office buildings since they provide considerable privacy while reducing glare.

Chapter: 10 Infiltration Heat Load and Weatherizing

Most older homes and some poorly constructed new ones have numerous cracks, holes, and openings through which cold outdoor air exchanges with the warm air inside a building in winter, and vice versa in summer. This uncontrolled entry of outside air into a building through unintentional openings is called infiltration, and it wastes a significant amount of energy since the air entering must be heated in winter and cooled in summer (Fig. 56). The warm air leaving the house represents energy loss. This is also the case for cool air leaving in summer since some electricity is used to cool that air. In homes that have not been properly weatherized, the air leaks account for about 30-40 percent of the total heat lost from the house in winter. That is, about one-third of the heating bill of such a house is due to the air leaks.

The rate of infiltration depends on the wind velocity and the temperature difference between the inside and the outside, and thus it varies throughout the year. The infiltration rates are much higher in winter than they are in summer because of the higher winds and larger temperature differences in winter. Therefore, distinction should be made between the design infiltration rate at design conditions, which is used to size heating or cooling equipment, and the seasonal average infiltration rate, which is used to properly estimate the seasonal energy consumption for heating or cooling. Infiltration appears to be providing “fresh outdoor air” to a building, but it is not a reliable ventilation mechanism since it depends on the weather conditions and the size and location of the cracks.

The air infiltration rate of a building can be determined by direct measurements by (1) injecting a tracer gas into a building and observing the decline of its concentration with time or (2) pressurizing the building to 10 to 75 Pa gage pressure by a large fan mounted on a door or window, and measuring the air flow required to maintain a specified indoor–outdoor pressure difference. The larger the air flow to maintain a pressure difference, the more the building may leak. Sulfur hexafluoride (SF₆) is commonly used as a tracer gas because it is inert, nontoxic, and easily detectable at concentrations as low as 1 part per billion. Pressurization testing is easier to conduct, and thus preferable to tracer gas testing. Pressurization test results for a whole house are given in Fig. 57. Despite their accuracy, direct measurement techniques are inconvenient, expensive, and time consuming. A practical alternative is to predict the air infiltration rate on the basis of extensive data available on existing buildings. One way of predicting the air infiltration rate is by determining the type and size of all the cracks at all possible locations (around doors and windows, lighting fixtures, wall–floor joints, etc., as shown in Fig. 58), as well as the pressure differential across the cracks at specified conditions, and calculating the air flow rates. This is known as the crack method.

A simpler and more practical approach is to “estimate” how many times the entire air in a building is replaced by the outside air per hour on the basis of experience with similar buildings under similar conditions. This is called the air-change method, and the infiltration rate in this case is expressed in terms of air changes per hour (ACH), defined as

The mass of air corresponding to 1 ACH is determined from m = rV where r is the density of air whose value is determined at the outdoor temperature and pressure. Therefore, the quantity ACH represents the number of building volumes of outdoor air that infiltrates (and eventually exfiltrates) per hour. At sea-level standard conditions of 1 atm (101.3 kPa or 14.7 psia) and 20°C (68°F), the density of air is

However, the atmospheric pressure and thus the density of air will drop by about 20 percent at 1500 m (5000 ft) elevation at 20°C, and by about 10 percent when the temperature rises to 50°C at 1 atm pressure. Therefore, local air density should be used in calculations to avoid such errors.

Infiltration rate values for hundreds of buildings throughout the United States have been measured during the last two decades, and the seasonal average infiltration rates have been observed to vary from about 0.2 ACH for newer energy-efficient tight buildings to about 2.0 ACH for older buildings. Therefore, infiltration rates can easily vary by a factor of 10 from one building to another. Seasonal average infiltration rates as low as 0.02 have been recorded. A study that involved 312 mostly new homes determined the average infiltration rate to be about 0.5 ACH. Another study that involved 266 mostly older homes determined the average infiltration rate to be about

0.9 ACH. The infiltration rates of some new office buildings with no outdoor air intake are measured to be between 0.1 and 0.6 ACH. Occupancy is estimated to add 0.1 to 0.15 ACH to unoccupied infiltration rate values. Also, the infiltration rate of a building can vary by a factor of 5, depending on the weather.

A minimum of 0.35 ACH is required to meet the fresh air requirements of residential buildings and to maintain indoor air quality, provided that at least 7.5 L/s (15 ft3/min) of fresh air is supplied per occupant to keep the indoor CO₂ concentration level below 1000 parts per million (0.1 percent). Usually the infiltration rates of houses are above 0.35 ACH, and thus we do not need to be concerned about mechanical ventilation. However, the infiltration rates of some of today’s energy-efficient buildings are below the required minimum, and additional fresh air must be supplied to such buildings by mechanical ventilation. It may be necessary to install a central ventilating system in addition to the bathroom and kitchen fans to bring the air quality to desired levels.

Venting the cold outside air directly into the house will obviously increase the heating load in winter. But part of the energy in the warm air vented out can be recovered by installing an air-to-air heat exchanger (also called an “economizer” or “heat recuperator”) that transfers the heat from the exhausted stale air to the incoming fresh air without any mixing (Fig. 59). Such heat exchangers are commonly used in superinsulated houses, but the benefits of such heat exchangers must be weighed against the cost and complexity of their installa- tion. The effectiveness of such heat exchangers is typically low (about 40 percent) because of the small temperature differences involved.

The primary cause of excessive infiltration is poor workmanship, but it may also be the settling and aging of the house. Infiltration is likely to develop where two surfaces meet such as the wall–foundation joint. Large differences between indoor and outdoor humidity and temperatures may aggravate the problem. Winds exert a dynamic pressure on the house, which forces the outside air through the cracks inside the house.

Infiltration should not be confused with ventilation, which is the intentional and controlled mechanism of air flow into or out of a building. Ventilation can be natural or forced (or mechanical), depending on how it is achieved. Ventilation accomplished by the opening of windows or doors is natural ventilation, whereas ventilation accomplished by an air mover such as a fan is forced ventilation. Forced ventilation gives the designer the greatest control over the magnitude and distribution of air flow throughout a building. The airtightness or air exchange rate of a building at any given time usually includes the effects of natural and forced ventilation as well as infiltration.

Air exchange, or the supply of fresh air, has a significant role on health, air quality, thermal comfort, and energy consumption. The supply of fresh air is a double-edged sword: too little of it will cause health and comfort problems such as the sick-building syndrome that was experienced in super-airtight buildings, and too much of it will waste energy. Therefore, the rate of fresh air supply should be just enough to maintain the indoor air quality at an acceptable level. The infiltration rate of older buildings is several times the required minimum flow rate of fresh air, and thus there is a high energy penalty associated with it. Infiltration increases the energy consumption of a building in two ways: First, the incoming outdoor air must be heated (or cooled in summer) to the indoor air temperature. This represents the sensible heat load of infiltration and is expressed as

where r_o is the density of outdoor#  air; c_p is the specific heat of air (about 1 kJ/kg · °C or 0.24 Btu/lbm · °F); V = (ACH)(V_building) is the volumetric flow rate of air, which is the number of air changes per hour times the volume of the building; and T_i – T_o is the temperature difference between the indoor and outdoor air. Second, the moisture content of outdoor air, in general, is different than that of indoor air, and thus the incoming air may need to be humidified or dehumidified. This represents the latent heat load of infiltration and is expressed as (Fig. 60)

where h_fg is the latent heat of vaporization at the indoor temperature (about 2340 kJ/kg or 1000 Btu/lbm) and v_i – v_o is the humidity ratio difference between the indoor and outdoor air, which can be determined from the psychrometric charts. The latent heat load is particularly significant in summer months in hot and humid regions such as Florida and coastal Texas. In winter, the humidity ratio of outdoor air is usually much lower than that of indoor air, and the latent infiltration load in this case represents the energy needed to vaporize the required amount of water to raise the humidity of indoor air to the desired level.

Preventing Infiltration

Infiltration accounts for a significant part of the total heat loss, and sealing the sites of air leaks by caulking or weather-stripping should be the first step to reduce energy waste and heating and cooling costs. Weatherizing requires some work, of course, but it is relatively easy and inexpensive to do.

Caulking can be applied with a caulking gun inside and outside where two stationary surfaces such as a wall and a window frame meet. It is easy to apply and is very effective in fixing air leaks. Potential sites of air leaks that can be fixed by caulking are entrance points of electrical wires, plumbing, and telephone lines; the sill plates where walls meet the foundation; joints between exterior window frames and siding; joints between door frames and walls; and around exhaust fans.

Weather-stripping is a narrow piece of metal, vinyl, rubber, felt, or foam that seals the contact area between the fixed and movable sections of a joint. Weather-stripping is best suited for sites that involve moving parts such as doors and windows. It minimizes air leakage by closing off the gaps between the moving parts and their fixed frames when they are closed. All exterior doors and windows should be weatherized. There are various kinds of weather-stripping, and some kinds are more suitable for particular kinds of gaps. Some common types of weather-stripping are shown in Fig. 61.

Chapter: 11 Annual Energy Consumption

In the thermal analysis of buildings, two quantities of major interest are (1) the size or capacity of the heating and the cooling system and (2) the annual energy consumption. The size of a heating or cooling system is based on the most demanding situations under the anticipated worst weather conditions, whereas the average annual energy consumption is based on average usage situations under average weather conditions. Therefore, the calculation procedure of annual energy usage is quite different than that of design heating or cooling loads.

An analysis of annual energy consumption and cost usually accompanies the design heat load calculations and plays an important role in the selection of a heating or cooling system. Often a choice must be made among several systems that have the same capacity but different efficiencies and initial costs. More efficient systems usually consume less energy and money per year, but they cost more to purchase and install. The purchase of a more efficient but more expensive heating or cooling system can be economically justified only if the system saves more in the long run from energy costs than its initial cost differential.

The impact on the environment may also be an important consideration on the selection process: A system that consumes less fuel pollutes the environment less, and thus reduces all the adverse effects associated with environmental pollution. But it is difficult to quantify the environmental impact in an economic analysis unless a price is put on it.

One way of reducing the initial and operating costs of a heating or cooling system is to compromise the thermal comfort of occupants. This option should be avoided, however, since a small loss in employee productivity due to thermal discomfort can easily offset any potential gains from reduced energy use. The U.S. Department of Energy periodically conducts comprehensive energy surveys to determine the energy usage in residential as well as nonresidential buildings and the industrial sector. Two 1983 reports (DOE/EIA-0246 and DOE/EIA-0318) indicate that the national average natural gas usage of all commercial buildings in the United States is 70,000 Btu/ft2 · year, which is worth about $0.50/ft2 or $5/m2 per year. The reports also indicate that the  average annual electricity consumption of commercial buildings due to air- conditioning is about 12 kWh/ft2 · year, which is worth about $1/ft2 or $10/m2 per year. Therefore, the average cost of heating and cooling of commercial buildings is about $15/m2 per year. This corresponds to $300/year for a 20 m2 floor space, which is large enough for an average office worker. But noting that the average salary and benefits of a worker are no less than $30,000 a year, it appears that the heating and cooling cost of a commercial building constitutes about 1 percent of the total cost (Fig. 63). Therefore, even a 1 percent loss in productivity due to thermal discomfort may cost the business owner more than the entire cost of energy. Likewise, the loss of business in retail stores due to unpleasant thermal conditions will cost the store owner many times what he or she is saving from energy. Thus, the message to the HVAC engineer is clear: in the design of heating and cooling systems of commercial buildings, treat the thermal comfort conditions as design constraints rather than as variables. The cost of energy is a very small fraction of the goods and services produced, and thus, do not incorporate any energy conservation measures that may result in a loss of productivity or loss of revenues.

When trying to minimize annual energy consumption, it is helpful to have a general idea about where most energy is used. A breakdown of energy usage in residential and commercial buildings is given in Fig. 64. Note that space heating accounts for most energy usage in all buildings, followed by water heating in residential buildings and lighting in commercial buildings. Therefore, any conservation measure dealing with them will have the greatest impact.

For existing buildings, the amount and cost of energy (fuel or electricity) used for heating and cooling of a building can be determined by simply analyzing the utility bills for a typical year. For example, if a house uses natural gas for space and water heating, the natural gas consumption for space heating can be determined by estimating the average monthly usage for water heating from summer bills, multiplying it by 12 to estimate the yearly usage, and subtracting it from the total annual natural gas usage. Likewise, the annual electricity usage and cost for air-conditioning can be determined by simply evaluating the excess electricity usage during the cooling months and adding them up. If the bills examined are not for a typical year, corrections can be made by comparing the weather data for that year to the average weather data.

For buildings that are at the design or construction stage, the evaluation of annual energy consumption involves the determination of (1) the space load for heating or cooling due to heat transfer through the building envelope and infiltration, (2) the efficiency of the furnace where the fuel is burned or the COP of cooling or heat pump systems, and (3) the parasitic energy consumed by the distribution system (pumps or fans) and the energy lost or gained from 

the pipes or ducts (Fig. 65). The determination of the space load is similar to the determination of the peak load, except the average conditions are used for the weather instead of design conditions. The space heat load is usually based on the average temperature difference between the indoors and the outdoors, but internal heat gains and solar effects must also be considered for better accuracy. Very accurate results can be obtained by using hourly data for a whole year and by making a computer simulation using one of the commercial building energy analysis software packages.

The simplest and most intuitive way of estimating the annual energy consumption of a building is the degree-day (or degree-hour) method, which is a steady-state approach. It is based on constant indoor conditions during the heating or cooling season and assumes the efficiency of the heating or cooling equipment is not affected by the variation of outdoor temperature. These conditions will be closely approximated if all the thermostats in a building are set at the same temperature at the beginning of a heating or cooling season and are never changed, and a seasonal average efficiency is used (rather than the full-load or design efficiency) for the furnaces or coolers.

You may think that anytime the outdoor temperature T_o drops below the indoor temperature T_i at which the thermostat is set, the heater will turn on to make up for the heat losses to the outside. However, the internal heat generated by people, lights, and appliances in occupied buildings as well as the heat gain from the sun during the day, Q_gain, will be sufficient to compensate for the heat losses from the building until the outdoor temperature drops below a certain value. The outdoor temperature above which no heating is required is called the balance point temperature T_balance (or the base temperature) and is determined from (Fig. 66)

where K_overall is the overall heat transfer coefficient of the building in W/°C or Btu/h · °F. There is considerable uncertainty associated with the determination of the balance point temperature, but based on the observations of typical buildings, it is usually taken to be 18°C in Europe and 65°F (18.3°C) in the United States for convenience. The rate of energy consumption of the heating system is

where h_heating is the efficiency of the heating system, which is equal to 1.0 for electric resistance heating systems, COP for the heat pumps, and combustion efficiency (about 0.6 to 0.95) for furnaces. If K_overall, T_balance, and h_heating, are taken to be constants, the annual energy consumption for heating can be determined by integration (or by summation over daily or hourly averages) as

where DD_heating is the heating degree-days. The + sign above the parenthesis indicates that only positive values are to be counted, and the temperature difference is to be taken to be zero when T_o > T_balance. The number of degree- days for a heating season is determined from

where DD_heating is the heating degree-days. The + sign above the parenthesis indicates that only positive values are to be counted, and the temperature difference is to be taken to be zero when T_o > T_balance. The number of degree- days for a heating season is determined from

where T_{o, avg, day} is the average outdoor temperature for each day (without considering temperatures above T_balance), and the summation is performed daily (Fig. 67). Similarly, we can also define heating degree-hours by using hourly average outdoor temperatures and performing the summation hourly. Note that the number of degree-hours is equal to 24 times the number of degree-days. Heating degree-days for each month and the yearly total for a balance point temperature of 65°F are given in Table 5 for several cities. Cooling degree-days are defined in the same manner to evaluate the annual energy consumption for cooling, using the same balance point temperature.   # Expressing the design energy consumption of a building for heating as Q_design = K_overall(T_i – T_o)_design/h_heating and comparing it to the annual energy consumption gives the following relation between energy consumption at designed conditions and the annual energy consumption (Table 22), where (T_i – T_o)_design is the design indoor–outdoor temperature difference.

Despite its simplicity, remarkably accurate results can be obtained with the degree-day method for most houses and single-zone buildings using a hand calculator. Besides, the degree-days characterize the severity of the weather at a location accurately, and the degree-day method serves as a valuable tool for gaining an intuitive understanding of annual energy consumption. But when the efficiency of the HVAC equipment changes considerably with the outdoor temperature, or the balance-point temperature varies significantly with time, it may be necessary to consider several bands (or “bins”) of outdoor temperatures and to determine the energy consumption for each band using the equipment efficiency for those outdoor temperatures and the number of hours those temperatures are in effect. Then the annual energy consumption is obtained by adding the results of all bands. This modified degree-day approach is known as the bin method, and the calculations can still be performed using a hand calculator.

The steady-state methods become too crude and unreliable for buildings that experience large daily fluctuations, such as a typical, well-lit, crowded office building that is open Monday through Friday from 8 _AM to 5 _PM. This is especially the case when the building is equipped with programmable thermostats that utilize night setback to conserve energy. Also, the efficiency of a heat pump varies considerably with the outdoor temperatures, and the efficiencies of boilers and chillers are lower at part load. Further, the internal heat gain and necessary ventilation rate of commercial buildings vary greatly with occupancy. In such cases, it may be necessary to use a dynamic method such as the transfer function method to predict the annual energy consumption accurately. Such dynamic methods are based on performing hourly calculations for the entire year and adding the results. Obviously they require the use of a computer with a well-developed and hopefully user-friendly program. Very accurate results can be obtained with dynamic methods since they consider the hourly variation of indoor and outdoor conditions as well as the solar radiation, the thermal inertia of the building, the variation of the heat loss coefficient of the building, and the variation of equipment efficiency with outdoor temperatures. Even when a dynamic method is used to determine the annual energy consumption, the simple degree-day method can still be used as a check to ensure that the results obtained are in the proper range.

Some simple practices can result in significant energy savings in residential buildings while causing minimal discomfort. The annual energy consumption can be reduced by up to 50 percent by setting the thermostat back in winter and up in summer, and setting it back further at nights (Table 23). Reducing the thermostat setting in winter by 4F (2.2C) alone can save 12 to 18 percent; setting the thermostat back by 10F (5.6C) alone for 8 h on winter nights can save 7 to 13 percent. Setting the thermostat up in summer by 4F (2.2C) can reduce the energy consumption of residential cooling units by 18 to 32 percent. Cooling energy consumption can be reduced by up to 25 percent by sun-screening and by up to 9 percent by attic ventilation (ASHRAE Handbook of Fundamentals, p. 28.14).

Summary

In a broad sense, air-conditioning means to condition the air to the desired level by heating, cooling, humidifying, dehumidifying, cleaning, and deodorizing. The purpose of the air- conditioning system of a building is to provide complete thermal comfort for its occupants. The metabolic heat generated in the body is dissipated to the environment through the skin and lungs by convection and radiation as sensible heat and by evaporation as latent heat. The total sensible heat loss can be expressed by combining convection and radiation heat losses as 

where R_clothing is the unit thermal resistance of clothing, which involves the combined effects of conduction, convection, and radiation between the skin and the outer surface of clothing. The operative temperature T_operative is approximately the arithmetic average of the ambient and surrounding surface temperatures. Another environmental index used in thermal comfort analysis is the effective temperature, which combines the effects of temperature and humidity.

The desirable ranges of temperatures, humidities, and ventilation rates for indoors constitute the typical indoor design conditions. The set of extreme outdoor conditions under which a heating or cooling system must be able to maintain a building at the indoor design conditions is called the outdoor design conditions. The heating or cooling loads of a building repre- sent the heat that must be supplied to or removed from the interior of a building to maintain it at the desired conditions. The effect of solar heating on opaque surfaces is accounted for by replacing the ambient temperature in the heat transfer rela- tion through the walls and the roof by the sol-air temperature, which is defined as the equivalent outdoor air temperature that gives the same rate of heat flow to a surface as would the combination of incident solar radiation, convection with the ambient air, and radiation exchange with the sky and the surrounding surfaces.

Heat flow into an exterior surface of a building subjected to solar radiation can be expressed as

where

and a_s is the solar absorptivity and e is the emissivity of the surface, h_o is the combined convection and radiation heat trans- fer coefficient, and q_solar is the solar radiation incident on the surface.

The conversion of chemical or electrical energy to thermal energy in a building constitutes the internal heat gain of a building. The primary sources of internal heat gain are people, lights, appliances, and miscellaneous equipment such as computers, printers, and copiers. The average amount of heat given off by a person depends on the level of activity and can range from about 100 W for a resting person to more than 500 W for a physically very active person. The heat gain due to a motor inside a conditioned space can be expressed as

W_motor is the power rating of the motor, f_load is the load factor of the motor during operation, f_usage is the usage  factor, and h_motor is the motor efficiency.

Under steady conditions, the rate of heat transfer through any section of a building wall or roof can be determined from

where T_i and T_o are the indoor and outdoor air temperatures, A_s is the heat transfer area, U is the overall heat transfer coefficient (the U-factor), and R = 1/U is the overall unit thermal resistance (the R-value). The overall R-value of a wall or roof can be determined from the thermal resistances of the individual components using the thermal resistance network. The effective emissivity of a plane-parallel air space is given by

where e₁ and e₂ are the emissivities of the surfaces of the air space.

Heat losses through the below-grade section of a basement wall and through the basement floor are given as

where U_{wall, ave} is the average overall heat transfer coefficient between the basement wall and the surface of the ground and U_floor is the overall heat transfer coefficient at the basement floor. Heat loss from floors that sit directly on the ground at or slightly above the ground level is mostly through the perimeter to the outside air rather than through the floor into the ground and is expressed as

where U_grade represents the rate of heat transfer from the slab per unit temperature difference between the indoor temperature T_indoor and the outdoor temperature T_outdoor and per unit length
of the perimeter p_floor of the building. When the crawl space temperature is known, heat loss through the floor of the building is determined from

where U_{building floor} is the overall heat transfer coefficient for the floor.

Windows are considered in three regions when analyzing heat transfer through them: (1) the center-of-glass, (2) the edge-of-glass, and (3) the frame regions. Total rate of heat transfer through the window is determined by adding the heat transfer through each region as

where

is the U-factor or the overall heat transfer coefficient of the window; A_window is the window area; A_center, A_edge, and A_frame are the areas of the center, edge, and frame sections of the window, respectively; and U_center, U_edge, and U_frame are the heat transfer coefficients for the center, edge, and frame sections of the window.

The sum of the transmitted solar radiation and the portion of the absorbed radiation that flows indoors constitutes the solar heat gain of the building. The fraction of incident solar radia- tion that enters through the glazing is called the solar heat gain coefficient SHGC, and the total solar heat gain through that window is determined from

where A_glazing is the glazing area of the window and q_{solar, incident}  is the solar heat flux incident on the outer surface of the window. Using the standard 3-mm-thick double-strength clear window glass sheet whose SHGC is 0.87 as the reference glazing, the shading coefficient SC is defined as

Shading devices are classified as internal shading and external shading, depending on whether the shading device is placed inside or outside.

The uncontrolled entry of outside air into a building through unintentional openings is called infiltration, and it wastes a significant amount of energy since the air entering must be heated in winter and cooled in summer. The sensible and latent heat load of infiltration are expressed as

where r_o is the density of outdoor air; c_p is the specific heat of air (about 1 kJ/kg · °C or 0.24 Btu/lbm · °F); V = (ACH) X (V_building) is the volumetric flow rate of air, which is the number of air changes per hour times the volume of the building; and T_i – T_o is the temperature difference between the indoor and outdoor air.

Also, h_fg is the latent heat of vaporization at indoor temperature (about 2340 kJ/kg or 1000 Btu/lbm) and v_i – v_o is the humidity ratio difference between the indoor and outdoor air.

The annual energy consumption of a building depends on the space load for heating or cooling, the efficiency of the heat- ing or cooling equipment, and the parasitic energy consumed by the pumps or fans and the energy lost or gained from the pipes or ducts. The annual energy consumption of a building can be estimated using the degree-day method as

where DDheating is the heating degree-days, K_overall is the overall heat transfer coefficient of the building in W/°C or Btu/h · °F, and h_heating is the efficiency of the heating system, which is equal to 1.0 for electric resistance heating systems, COP for the heat pumps, and combustion efficiency (about 0.6 to 0.95) for furnaces.