Introduction

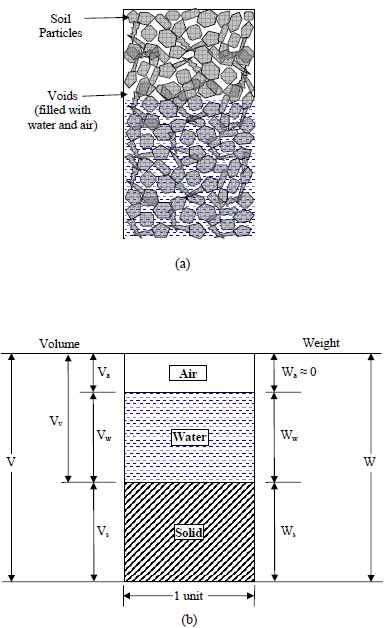
Soil mass is generally a three phase system that consists of solid particles, liquid and gas. The liquid and gas phases occupy the voids between the solid particles as shown in Figure 1a. For practical purposes, the liquid may be considered to be water (although in some cases the water may contain some dissolved salts or pollutants) and the gas as air. Soil behavior is controlled by the interaction of these three phases. Due to the three phase composition of soils, complex states of stresses and strains may exist in a soil mass. Proper quantification of these states of stress, and their corresponding strains, is a key factor in the design and construction of transportation facilities.

The first step in quantification of the stresses and strains in soils is to characterize the distribution of the three phases of the soil mass and determine their inter-relationships. The inter-relationships of the weights and volumes of the different phases are important since they not only help define the physical make-up of a soil but also help determine the in-situ geostatic stresses, i.e., the states of stress in the soil mass due only to the soil’s self-weight. The volumes and weights of the different phases of matter in a soil mass shown in Figure 21a can be represented by the block diagram shown in Figure 1b. Such a diagram is also known as a phase diagram. A block of unit cross sectional area is considered. The symbols for the volumes and weights of the different phases are shown on the left and right sides of the block, respectively. The symbols for the volumes and weights of the three phases are defined as follows:

• V_a, W_a : volume, weight of air phase. For practical purposes, W_a = 0.
• V_w, W_a: volume, weight of water phase.
• V_v, W_a : volume, weight of total voids. For practical purposes, W_v = W_w as W_a = 0.
• V_s, W_s : volume, weight of solid phase.
• V, W : volume, weight of the total soil mass .

Although W_a = 0 so that W_a = W_a, V_a is generally > 0 and must always be taken into account. Since the relationship between V_a and V_a usually changes with groundwater conditions as well as under imposed loads, it is convenient to designate all the volume not occupied by the solid phase as void space, Vv. Thus, V_a = V_a + V_a. Use of the terms illustrated in Figure 1b, allows a number of basic phase relationships to be defined and/or derived as discussed next.

1.0 Basic Weight-Volume Relationships

Various volume change phenomena encountered in geotechnical engineering, e.g., compression, consolidation, collapse, compaction, expansion, etc. can be described by expressing the various volumes illustrated in Figure 1b as a function of each other. Similarly, the in-situ stress in a soil mass is a function of depth and the weights of the different soil elements within that depth. This in-situ stress, also known as overburden stress (see Section 3), can be computed by expressing the various weights illustrated in Figure 1b as a function of each other. This section describes the basic inter-relationships among the various quantities shown in Figure 1b.

1.1 Volume Ratios

A parameter used to express of the volume of the voids in a given soil mass can be obtained from the ratio of the volume of voids, V_v, to the total volume, V. This ratio is referred to as porosity, n, and is expressed as a percentage as follows:

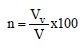
Obviously, the porosity can never be greater than 100%. As a soil mass is compressed, the volume of voids, V_v, and the total volume, V, decrease. Thus, the value of the porosity changes. Since both the numerator and denominator in Equation 1 change at the same time, it is difficult to quantify soil compression, e.g., settlement or consolidation, as a function of porosity. Therefore, in soil mechanics the volume of voids, V_v, is expressed in relation to a quantity, such as the volume of solids, V_s, that remains unchanging during consolidation or compression. This is done by the introduction of a quantity known as void ratio, e, which is expressed in decimal form as follows:

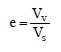
Unlike the porosity, the void ratio can have values greater than 1. That would mean that the soil has more void volume than solids volume, which would suggest that the soil is “loose” or “soft.” Therefore, in general, the smaller the value of the void ratio, the denser the soil. As a practicality, for a given type of coarse-grained soil, such as sand, there is a minimum and maximum void ratio. These values can be used to evaluate the relative density, Dr (%), of that soil at any intermediate void ratio as follows:

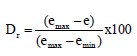
At e = e_max the soil is as loose as it can get and the relative density equals zero. At e = e_min the soil is as dense as it can get and the relative density equals 100%. Relative density and void ratio are particularly useful index properties since they are general indicators of the relative strength and compressibility of the soil sample, i.e., high relative densities and low void ratios generally indicate strong or incompressible soils; low relative densities and high void ratios may indicate weak or compressible soils.

While the expressions for porosity and void ratio indicate the relative volume of voids, they do not indicate how much of the void space, V_v, is occupied by air or water. In the case of a saturated soil, all the voids (i.e., soil pore spaces) are filled with water, V_v = V_w. While this condition is true for many soils below the ground water table or below standing bodies of water such as rivers, lakes, or oceans, and for some fine-grained soils above the ground water table due to capillary action, the condition of most soils above the ground water table is better represented by consideration of all three phases where voids are occupied by both air and water. To express the amount of void space occupied by water as a percentage of the total volume of voids, the term degree of saturation, S, is used as follows:

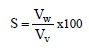
Obviously, the degree of saturation can never be greater than 100%. When S = 100%, all the void space is filled with water and the soil is considered to be saturated. When S = 0%, there is no water in the voids and the soil is considered to be dry.

1.2 Weight Ratios

While the expressions of the distribution of voids in terms of volumes are convenient for theoretical expressions, it is difficult to measure these volumes accurately on a routine basis. Therefore, in soil mechanics it is convenient to express the void space in gravimetric, i.e., weight, terms. Since, for practical purposes, the weight of air, W_a, is zero, a measure of the void space in a soil mass occupied by water can be obtained through an index property known as the gravimetric water or moisture content, w, expressed as a percentage as follows:

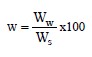
The word “gravimetric” denotes the use of weight as the basis of the ratio to compute water content as opposed to volume, which is often used in hydrology and the environmental sciences to express water content. Since water content is understood to be a weight ratio in geotechnical engineering practice, the word “gravimetric” is generally omitted. Obviously, the water content can be greater than 100%. This occurs when the weight of the water in the soil mass is greater than the weight of the solids. In such cases the void ratio of the soil is generally greater than 1 since there must be enough void volume available for the water so that its weight is greater than the weight of the solids. However, even if the water content is greater than 100%, the degree of saturation may not be 100% because the water content is a weight ratio while saturation is a volume ratio.

For a given amount of soil, the total weight of soil, W, is equal to W_s + W_w, since the weight of air, W_a, is practically zero. The water content, w, can be easily measured by oven-drying a given quantity of soil to a high enough temperature so that the amount of water evaporates and only the solids remain. By measuring the weight of a soil sample before and after it ahs been oven dried, both W and W_s, can be determined. The water content, w, can be determined as follows since W_a = 0:

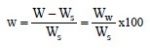
Most soil moisture is released at a temperature between 220 and 230oF (105 and 110oC). Therefore, to compare reported water contents on an equal basis between various soils and projects, this range of temperature is considered to be a standard range.

1.3 Weight-Volume Ratios (Unit Weights) and Specific Gravity

The simplest relationship between the weight and volume of a soil mass (refer to Figure 1b) is known as the total unit weight, γ_t, and is expressed as follows:

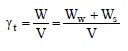
The total unit weight of a soil mass is a useful quantity for computations of vertical in-situ stresses. For a constant volume of soil, the total unit weight can vary since it does not account for the distribution of the three phases in the soil mass. Therefore the value of the total unit weight for a given soil can vary from its maximum value when all of the voids are filled with water (S=100%) to its minimum value when there is no water in the voids (S=0%). The former value is called the saturated unit weight, γ_sat; the latter value is referred to as the dry unit weight, γ_d. In terms of the basic quantities shown in Figure 1b and with reference to Equation 5, when W_w = 0 the dry unit weight, γ_d, can be expressed as follows:

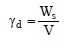
For computations involving soils below the water table, the buoyant unit weight is frequently used where:

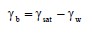
where, γ_w equals the unit weight of water and is defined as follows:

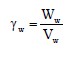
In the geotechnical literature, the buoyant unit weight, γ_b, is also known as the effective unit weight, γ’, or submerged unit weight, γ_sub. Unless there is a high concentration of dissolved salts, e.g., in sea water, the unit weight of water, γ_w, can be reasonably assumed to be 62.4 lb/ft³ (9.81 kN/m³).

To compare the properties of various soils, it is often instructive and preferable to index the various weights and volumes to unchanging quantities, which are the volume of solids, V_s, and the weight of solids, W_s. A ratio of W_s to V_s, is known as the unit weight of the solid phase, γ_s, and is expressed as follows:

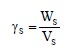
The unit weight of the solid phase, γ_s, should not be confused with the dry unit weight of the soil mass, γ_d, which is defined in Equation 6 as the total unit weight of the soil mass when there is no water in the voids, i.e., at S = 0%. The distinction between γ_s and γ_d is very subtle, but it is very important and should not be overlooked. For example, for a solid piece of rock (i.e., no voids) the total unit weight is γ_s while the total unit weight of a soil whose voids are dry is γ_d. In geotechnical engineering, γ_d is more commonly of interest than γ_s.

Since the value of γ_w is reasonably well known, the unit weight of solids, γ_s, can be expressed in terms of γ_w. The concept of Specific Gravity, G, is used to achieve this goal. In physics textbooks, G is defined as the ratio between the mass density of a substance and the mass density of some reference substance. Since unit weight is equal to mass density times the gravitational constant, G can also be expressed as the ratio between the unit weight of a substance and the unit weight of some reference substance. In the case of soils, the most convenient reference substance is water since it is one of the three phases of the soil and its unit weight is reasonably constant. Using this logic, the specific gravity of the soil solids, G_s, can be expressed as follows:

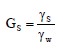
The bulk specific gravity of a soil is equal to γ_t / γ_w. The “bulk specific gravity” is not the same as G_s and is not very useful in practice since the γ_t of a soil can change easily with changes in void ratio and/or degree of saturation. Therefore, the bulk specific gravity is almost never used in geotechnical engineering computations.

The value of G_s can be determined in the laboratory, but it can usually be estimated with sufficient accuracy for various types of soil solids. For routine computations, the value of G_s for sands composed primarily of quartz particles may be taken as 2.65. Tests on a large number of clay soils indicate that the value of G_s for clays usually ranges from 2.5 to 2.9 with an average value of 2.7.

1.4 Determination and Use of Basic Weight-Volume Relations

The five relationships, n, e, w, γ_t and G_s, represent the basic weight-volume properties of soils and are used in the classification of soils and for the development of other soil properties. These properties and how they are obtained and applied in geotechnical engineering are summarized in Table 1. A summary of commonly used weight-volume (unit weight) relations that incorporate these terms is presented in Table 2.

1.5 Size of Grains in the Solid Phase

As indicated in Figure 1a, the solid phase is composed of soil grains. One of the major factors that affect the behavior of the soil mass is the size of the grains. The size of the grains may range from the coarsest (e.g., boulders, which can be 12- or more inches [300 mm] in diameter) to the finest (e.g., colloids, which can be smaller than 0.0002–inches [0.005 mm]). Since soil particles come in a variety of different shapes, the size of the grains is defined in terms of an effective grain diameter. The distribution of grain sizes in a soil mass is determined by shaking air-dried material through a stack of sieves having decreasing opening sizes. Table 3 shows U.S. standard sieve sizes and associated opening sizes. Sieves with opening size 0.25 in (6.35 mm) or less are identified by a sieve number which corresponds to the approximate number of square openings per linear inch of the sieve (ASTM E 11).

To determine the grain size distribution, the soil is sieved through a stack of sieves with each successive screen in the stack from top to bottom having a smaller (approximately half of the upper sieve) opening to capture progressively smaller particles. Figure 2 shows a selection of some sieves and starting from right to left soil particles retained on each sieve, except for the powdery particles shown on the far left, which are those that passed through the last sieve on the stack. The amount retained on each sieve is collected, dried and weighed to determine the amount of material passing that sieve size as a percentage of the total sample being sieved. Since electro-static forces impede the passage of finer-grained particles through sieves, testing of such particles is accomplished by suspending the chemically dispersed particles in a water column and measuring the change in specific gravity of the liquid as the particles fall from suspension. The change in specific gravity is related to the fall velocities of specific particle sizes in the liquid. This part of the test is commonly referred to as a hydrometer analysis. Because of the strong influence of electro-chemical forces on their behavior, colloidal sized particles may remain in suspension indefinitely (particles with sizes from 10^-3 mm to 10^-6 mm are termed “colloidal.”) Sample grain size distribution curves are shown in Figure 3. The nomenclature associated with various grain sizes (cobble, gravel, sand, silt or clay) is also shown in Figure 3. Particles having sizes larger than the No. 200 sieve (0.075 mm) are termed ”coarse-grained” while those with sizes finer than the No. 200 sieve are termed “fine-grained.”

The results of the sieve and hydrometer tests are represented graphically on a grain size distribution curve or gradation curve. As shown in Figure 3, an arithmetic scale is used on the ordinate (Y-axis) to plot the percent finer by weight and a logarithmic scale is used on the abscissa (X-axis) for plotting particle (grain) size, which is typically expressed in millimeters.

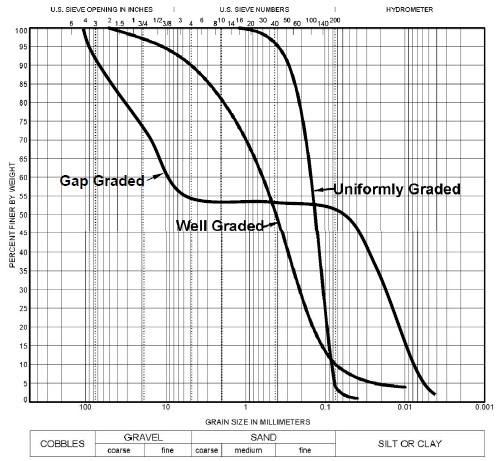
The logarithmic scale permits a wide range of particle sizes to be shown on a single plot. More importantly it extends the scale, thus giving all the grains sizes an approximately equal amount of separation on the X-axis. For example, a grain-size range of 4.75 mm (No.4 sieve) to 0.075 mm (No. 200 sieve) when plotted on an arithmetic scale, will have the 0.075 mm (No. 200 sieve), 0.105 mm (No. 140 sieve), and 0.150 mm (No. 100) particle size plot very close to each other. The logarithmic scale permits separation of grain sizes that makes it easier to compare the grain size distribution of various soils.

The shape of the grain size distribution curve is somewhat indicative of the particle size distribution as shown in Figure 3. For example,

• A smooth curve covering a wide range of sizes represents a well-graded or non-uniform soil.
• A vertical or near vertical slope over a relatively narrow range of particle sizes indicates that the soil consists predominantly of the particle sizes within that range of particle sizes. A soil consisting of particles having only a few sizes is called a poorly-graded or uniform soil.
• A curve that contains a horizontal or nearly horizontal portion indicates that the soil is deficient in the grain sizes in the region of the horizontal slope. Such a soil is called a gap-graded soil.

Well-graded soils are generally produced by bulk transport processes (e.g., glacial till). Poorly graded soils are usually sorted by the transporting medium e.g., beach sands by water; loess by wind. Gap-graded soils are also generally sorted by water, but certain sizes were not transported.

1.6 Shape of Grains in Solid Phase

The shape of individual grains in a soil mass plays an important role in the engineering characteristics (strength and stability) of the soil. Two general shapes are normally recognized, bulky and platy.

1.6.1 Bulky Shape

Cobbles, gravel, sand and some silt particles cover a large range of sizes as shown in Figure 2-; however, they are all bulky in shape. The term bulky is confined to particles that are relatively large in all three dimensions, as contrasted to platy particles, in which one dimension is small as compared to the other two, see Figure 4. The bulky shape has five subdivisions listed in descending order of desirability for construction

• Angular particles are those that have been freshly broken up and are characterized by jagged projections, sharp ridges, and flat surfaces. Angular gravels and sands are generally the best materials for construction because of their interlocking characteristics. Such particles are seldom found in nature, however, because physical and chemical weathering processes usually wear off the sharp ridges in a relatively short period time. Angular material is usually produced artificially, by crushing.
• Subangular particles are those that have been weathered to the extent that the sharper points and ridges have been worn off.
• Subrounded particles are those that have been weathered to a further degree than subangular particles. They are still somewhat irregular in shape but have no sharp corners and few flat areas. Materials with this shape are frequently found in stream beds. If composed of hard, durable particles, subrounded material is adequate for most construction needs.
• Rounded particles are those on which all projections have been removed, with few irregularities in shape remaining. The particles resemble spheres and are of varying sizes. Rounded particles are usually found in or near stream beds or beaches.
• Well rounded particles are rounded particles in which the few remaining irregularities have been removed. Like rounded particles, well rounded particles are also usually found in or near stream beds or beaches.

1.6.2 Platy Shape

Platy, or flaky, particles are those that have flat, plate like grains. Clay and some silts are common examples. Because of their shape, flaky particles have a greater surface area than bulky particles, assuming that the weights and volumes of the two are the same. For example, 1 gram of bentonite (commercial name for montmorillonite clay) has a surface area of approximately 950 yd2 (800 m2) compared to a surface area of approximately 0.035 yd2 (0.03 m2) of 1 gram of sand. Because of their mineralogical composition and greater specific surface area, most flaky particles also have a greater affinity for water than bulky particles. Due to the high affinity of such soils for water, the physical states of such fine-grained soils change with the amount of water in these soils. The effect of water on the physical states of fine grained soils is discussed next.

1.7 Effect of Water on Physical States of Soils

For practical purposes, the two most dominant phases are the solid phase and the water phase. It is intuitive that as the water content increases, the contacts between the particles comprising the solid phase will be “lubricated.” If the solid phase is comprised of coarse particles, e.g. coarse sand or gravels, then water will start flowing between the particles of the solid phase. If the solid phase is comprised of fine-grained particles, e.g., clay or silt, then water cannot flow as freely as in the coarse-grained solid phase because pore spaces are smaller and solids react with water. However, as the water content increases even the fine-grained solid phase will conduct water and under certain conditions the solid phase itself will start deforming like a viscous fluid, e.g., like a milk shake or a lava flow. The mechanical transformation of the fine-grained soils from a solid phase into a viscous phase is a very important concept in geotechnical engineering since it is directly related to the load carrying capacity of soils. It is obvious that the load carrying capacity of a solid is greater than that of water. Since water is contained in the void space, the effect of water on the physical states of fine-grained soils is important. Some of the basic index properties related to the effect of water are described next.

The physical and mechanical behavior of fine-grained-soils is linked to four distinct states: solid, semi-solid, plastic and viscous liquid in order of increasing water content. Consider a soil initially in a viscous liquid state that is allowed to dry uniformly. This state is shown as Point A in Figure 5, which shows a plot of total volume versus water content. As the soil dries, its water content reduces and consequently so does its total volume as the solid particles move closer to each other. As the water content reduces, the soil can no longer flow like a viscous liquid. Let us identify this state by Point B in Figure 5. The water content at Point B is known as the “Liquid Limit” in geotechnical engineering and is denoted by LL.

As the water content continues to reduce due to drying, there is a range of water content at which the soil can be molded into any desired shape without rupture. In this range of water content, the soil is considered to be “plastic.”

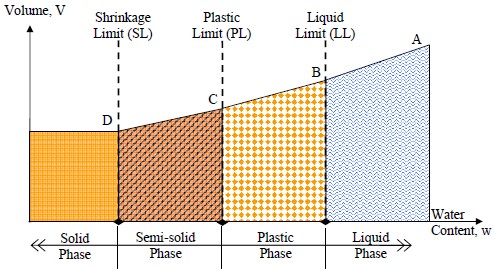
If the soil is allowed to dry beyond the plastic state, the soil cannot be molded into any shape without showing cracks, i.e., signs of rupture. The soil is then in a semi-solid state. The water content at which cracks start appearing when the soil is molded is known as the “Plastic Limit.” This moisture content is shown at Point C in Figure 5 and is denoted by PL. The difference in water content between the Liquid Limit and Plastic Limit, is known as the Plasticity Index, PI, and is expressed as follows:

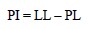
Since PI is the difference between the LL and PL, it denotes the range in water content over which the soil acts as a plastic material as shown in Figure 5.

As the soil continues to dry, it will be reduced to its basic solid phase. The water content at which the soil changes from a semi-solid state to a solid state is called the Shrinkage Limit, SL. No significant change in volume will occur with additional drying below the shrinkage limit. The shrinkage limit is useful for the determination of the swelling and shrinkage characteristics of soils.

The liquid limit, plastic limit and shrinkage limit are called Atterberg limits after A. Atterberg (1911), the Swedish soil scientist who first proposed them for agricultural applications.

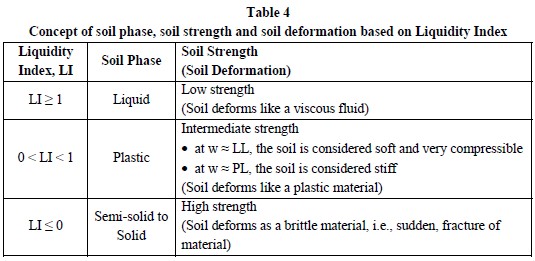
For foundation design, engineers are most interested in the load carrying capacity, i.e., strength, of the soil and its associated deformation. The soil has virtually no strength at the LL, while at water contents lower than the PL (and certainly below the SL) the soil may have considerable strength. Correspondingly, soil strength increases and soil deformation decreases as the water content of the soil reduces from the LL to the SL. Since the Atterberg limits are determined for a soil that is remolded, a connection needs to be made between these limits and the in-situ moisture content, w, of the soil for the limits to be useful in practical applications in foundation design. One way to quantify this connection is through the Liquidity Index, LI, that is given by:

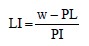
The liquidity index is the ratio of the difference between the soil’s in-situ water content and plastic limit to the soil’s plasticity index. The various phases shown in Figure 5 and anticipated deformation behavior can now be conveniently expressed in terms of LI as shown in Table 4.

Another valuable tool in assessing the characteristics of a fine-grained soil is to compare the LL and PI of various soils. Each fine-grained soil has a relatively unique value of LL and PI. A plot of PI versus LL is known as the Plasticity Chart (see Figure 6). Arthur Casagrande, who developed the concept of the Plasticity Chart, had noted the following during the First Pan American Conference on Soil Mechanics and Foundation Engineering (Casagrande, 1959).

I consider it essential that an experienced soils engineer should be able to judge the position of soils, from his territory, on a plasticity chart merely on the basis of his visual and manual examination of the soils. And more than that, the plasticity chart should be for him like a map of the world. At least for certain areas of the chart, that are significant for his activities, he should be well familiar. The position of soils within these areas should quickly convey to him a picture of the significant engineering properties that he should expect.

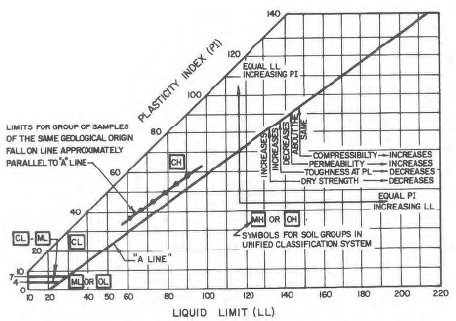
Casagrande proposed the inclusion of the A-line on the plasticity chart as a boundary between clay (above the A-line) and silt (below the A-line) to help assess the engineering characteristics of fine-grained soils. Once PI and LL are determined for a fine-grained soil at a specific site, a point can be plotted on the plasticity chart that will allow the engineer to develop a feel for the general engineering characteristics of that particular soil. The plasticity chart also permits the engineer to compare different soils across the project site and even between different project sites.

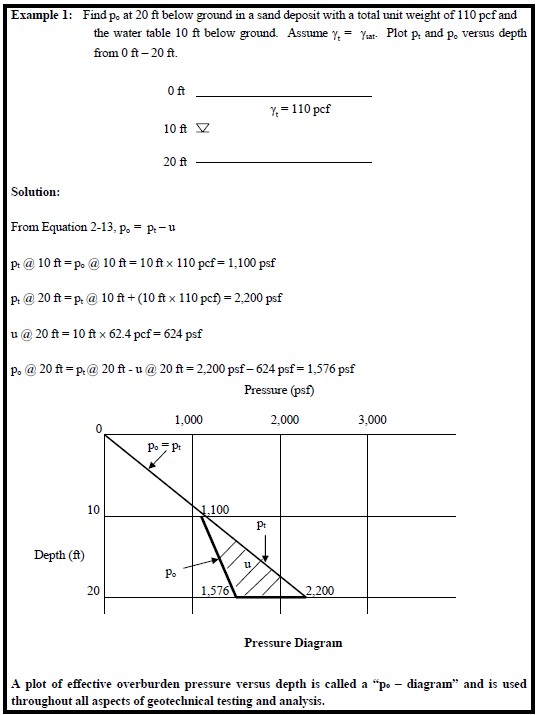
2.0 Principle of Effective Stress

The contacts between soil grains are effective in resisting applied stresses in a soil mass. Under an applied load, the total stress in a saturated soil sample is composed of the intergranular stress and the pore water pressure. When pore water drains from a soil, the contact between the soil grains increases, which increases the level of intergranular stress. This intergranular contact stress is called the effective stress. The effective stress, p_o, within a soil mass is the difference between the total stress, p_t, and pore water pressure, u. The principle of effective stress is a fundamental aspect of geotechnical engineering and is written as follows:

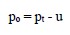
In general, soil deposits below the ground water table will be considered saturated and the ambient pore water pressure at any depth may be computed by multiplying the unit weight of water, γ_w, by the height of water above that depth. The total stress at that depth may be found by multiplying the total unit weight of the soil by the depth. The effective stress is the total stress minus the pore water pressure. This concept is used to construct the profile of pressure in the ground as a function of depth and is discussed next.

3.0 Overburden Pressure

Soils existing at a distance below ground are affected by the weight of the soil above that depth. The influence of this weight, known generally as overburden, causes a state of stress to exist, which is unique at that depth, for that soil. This state of stress is commonly referred to as the overburden or in-situ or geostatic state of stress. When a soil sample is removed from the ground, as during the field exploration phase of a project, that in-situ state of stress is relieved as all confinement of the sample has been removed. In laboratory testing, it is important to reestablish the in-situ stress conditions and to study changes in soil properties when additional stresses representing the expected design loading are applied. The stresses to be used during laboratory testing of soil samples are estimated from either the total or effective overburden pressure. The engineer’s first task is determining the total and effective overburden pressure variation with depth. This relatively simple task involves estimating the average total unit weight for each soil layer in the soil profile, and determining the depth of the water table. Unit weight may be reasonably well estimated from tests on undisturbed samples or from standard penetration N-values and visual soil identification. The water table depth, which is typically recorded on boring logs, can be used to compute the hydrostatic pore water pressure at any depth. The total overburden pressure, p_t, is found by multiplying the total unit weight of each soil layer by the corresponding layer thickness and continuously summing the results with depth. The effective overburden pressure, p_o, at any depth is determined by accumulating the weights of all layers above that depth with consideration of the water level conditions at the site as follows:

Soils above the water table

• Multiply the total unit weight by the thickness of each respective soil layer above the desired depth, i.e., p_o = p_t.

Soils below the ground water table

• Compute pore water pressure u as z_w γ_w where z_w is the depth below ground watertable and γw is the unit weight of water
• To obtain effective overburden pressure, p_o, subtract pore water pressure, u, from p_t
• For soils below the ground water table, p_t is generally assumed to be equal to p_sat

Alternatively, the following approach can be used:

• Reduce the total unit weights of soils below the ground water table by the unit weight of water (62.4 pcf (9.8 kN/m³)), i.e., use effective unit weights, γ’, and multiply by the thickness of each respective soil layer between the water table and the desired depth below the ground water table, i.e., p_o = (γ_t -γ_w ) (depth), or γ’ (depth).

In the geotechnical literature, the effective unit weight, γ’, is also known as the buoyant unit weight or submerged unit weight and symbols, γb or γsub, respectively are used.

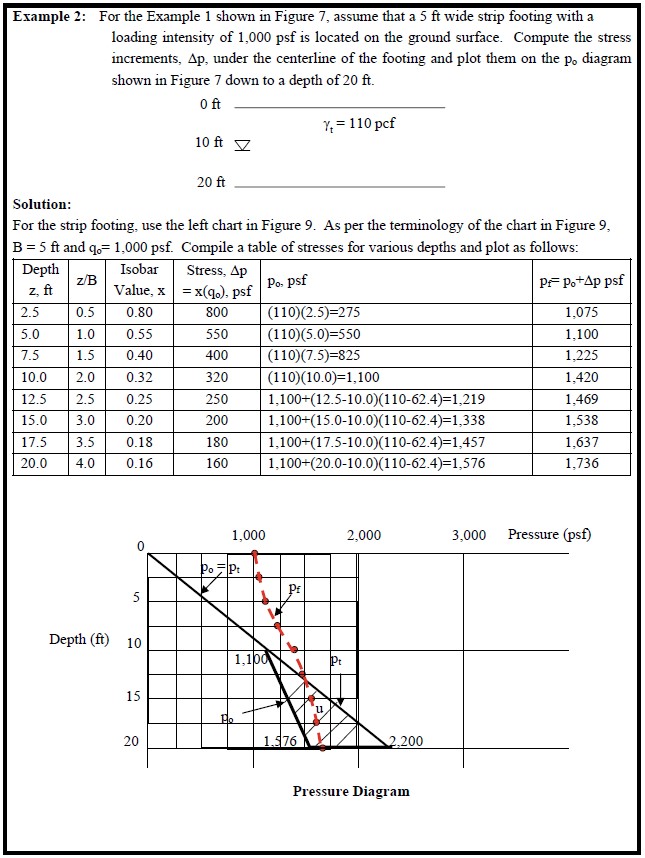
An example is solved in Figure 7.

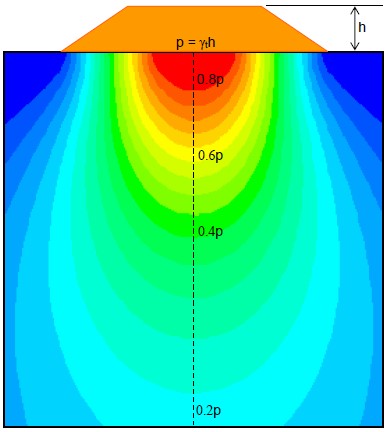
4.0 Vertical Stress Distribution in Soil Due to External Loadings

When a load is applied to the soil surface, it increases the vertical and lateral stresses within the soil mass. The increased stresses are greatest directly under the loaded area and dissipate within the soil mass as a function of distance away from the loaded area. This is commonly called spatial attenuation of applied loads. A schematic of the vertical stress distribution with depth along the centerline under an embankment of height, h, constructed with a soil having total unit weight, γ_t, is shown in Figure 8.

Estimation of vertical stresses at any point in a soil mass due to external loadings are of great significance in the prediction of volume change of soils (e.g., settlement) under buildings, bridges, embankments and many other structures. The computation of the total vertical stress change induced by an external loading will depend on the configuration of the external loads. Common examples of the external loads are as follows:

• Uniform strip loads such as the load on a long wall footing of sufficient width,
• Uniformly loaded square, rectangular or circular footings such as column footings of buildings, pier footings, footings for water tanks, mats, etc., and
• Triangular and/or trapezoidal strip loads such as the loads of long earth embankments.

The theory of elasticity is often used to compute the stresses induced within a soil mass by external loadings. The most widely used elastic formulae were first developed by Boussinesq (1885) for point loads acting at the surface of a semi-infinite elastic half-space. These formulae, often known as Boussinesq solutions, can be integrated to give stresses below external loadings acting on a finite area. The basic assumptions in these formulae are (a) the stress is proportional to strain, (b) the soil is homogeneous (i.e., the properties are constant throughout the soil mass), and (c) the soil is isotropic (i.e., the properties are the same in all directions through a point). Westergaard (1938) modified the Boussinesq solutions by assuming that the semi-infinite elastic half-space is interspersed with infinitely thin but perfectly rigid layers that allow vertical movement but no lateral movement. In reality, a soil mass never fulfills the assumptions of either of these idealized solutions. Nevertheless, these elastic solutions, with appropriate modifications and judgment, have been found to yield acceptable approximate estimates of stresses in the soil mass and are widely used in geotechnical engineering practice. The Boussinesq solutions are generally used in most situations, even those where layered soils are encountered provided the thickness of the layers is on the order of a few feet or more. On the other hand, the Westergaard solutions are usually used for varved clays where the predominant soil mass is clay interspersed with thin layers of sand whose thickness is on the order of inches.

The derivations of the equations for various common loadings cited above are tedious. They are omitted in this course so that the reader can concentrate on the use of published solutions, generally in the form of charts. The following sections contain the chart solutions for some of the loadings most commonly encountered in practice. Caution in the use of these charts is advised since they all pertain to stress increments at very well-defined points within the soil mass due to the applied pressures indicated. The total stress acting at a point of interest is equal to the stress increment at that point due to the newly applied load plus existing stresses at that point due to the geostatic stress and stresses due to other external loads applied previously.

4.1 Uniformly Loaded Continuous (Strip) and Square Footings

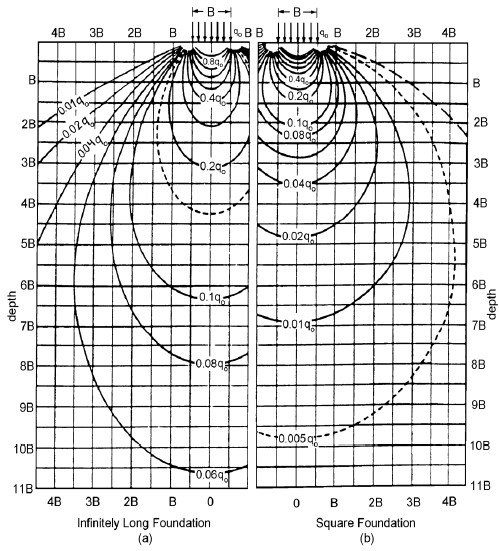
A loaded area is considered to be infinitely long when its length, L, to width, B, ratio is greater than or equal to 10, i.e., L/B ≥ 10. The load on such an area is commonly known as a strip load. Figure 9 presents vertical pressure isobars under strip and square footings based on Boussinesq’s theory. An isobar is a line that connects all points of equal stress increment below the ground surface. In other words, an isobar is a stress increment contour.

Each isobar represents a fraction of the stress applied at the surface and delineates the zone of influence of the footing such that the area contained within two adjacent isobars experiences stresses greater than the lower isobar and less than the upper isobar. Since these isobars form closed figures that resemble the form of a bulb, they are also termed bulbs of pressure or simply the pressure bulbs. The pressure bulb concept gives the user a feel for the spread of the stresses through a soil mass.

According to linear elastic theory, the size of the pressure bulb is proportional to the size of the loaded area. This is a key concept in geotechnical engineering that is used to evaluate the depth of significant influence, DOSI, denoted by DS of an applied surface load. The depth DS is a finite depth below which there are no significant strains in the soil mass due to the loads imposed at the surface. Typically, strains are not significant once the stresses have attenuated to a value of 10 to 15% of those at the surface. For example, Figure 9a shows that for “infinitely long” strip footings, DS = 4 to 6B, while for square footings, Figure 9b shows that DS = 1.5 to 2B. The depths corresponding to this 10 to 15% criterion can be used to determine the minimum depth of field exploration for proposed strip or square footings to ensure that the anticipated significant depth is explored.

It may be seen from Figure 9 that the effect of the vertical stresses extends laterally beyond the width of the loaded area, B. This observation is very useful in assessing the influence of one loaded area on the other. Alternatively, this observation can be used to determine an adequate spacing between adjacent loaded areas. It also indicates that the effect of construction activities may be felt beyond a specific site. Such effects should be evaluated before construction so that mitigation measures can be taken to avoid legal implications.

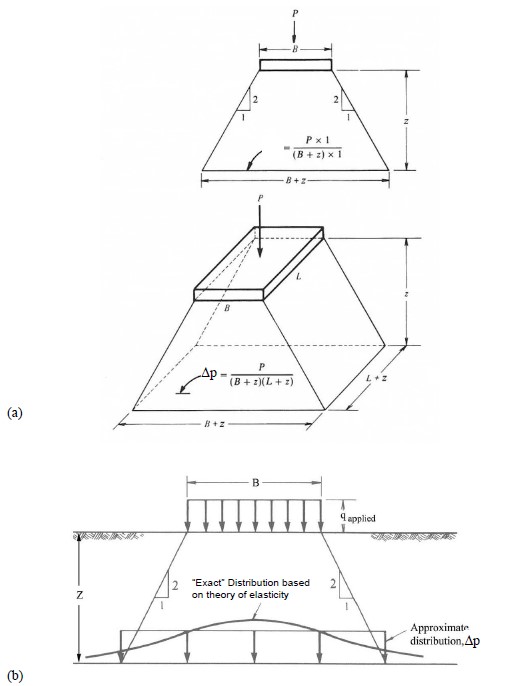
4.2 Approximate (2:1) Stress Distribution Concept

As an approximation to the exact solution given by the Boussinesq charts, the total load at the surface of the soil mass may be distributed over an area of the same shape as the loaded area on the surface, but with dimensions that increase with depth at a rate of one horizontal unit for every two vertical units. This is illustrated in Figure 10, which shows a rectangular area of dimensions B x L at the surface. At a depth, z, the total load is assumed to be uniformly distributed over an area (B+z) by (L+z). Since the stress is distributed at the rate of 2:1 (vertical:horizontal), this approximation method it is commonly known as the “2:1 stress distribution” method.

The relationship between the approximate distribution of stress determined by this method and the exact distribution is illustrated in Figure 10. In this figure, the vertical stress distribution at a depth B below a uniformly loaded square area of width B is shown along a horizontal line that passes beneath the center of the area and extends beyond the edges of the loaded area. Also shown is the approximate uniform distribution at depth B determined by the 2:1 stress distribution method described above. The discrepancy between the two methods decreases as the ratio of the depth considered to the size of the loaded area increases (Perloff and Baron, 1976).

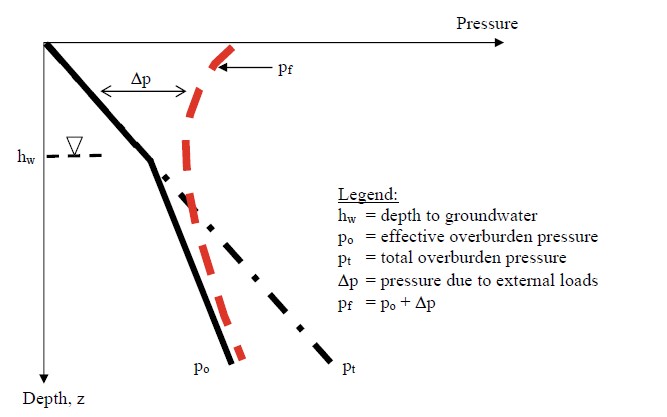
5.0 Representation of Imposed Pressures on the P_o Diagram

The pressure distributions computed by using the charts in Section 4, can be shown superimposed on the p_o diagram as shown in Figure 7. As discussed in the previous sections, an applied pressure at the surface causes stress increments within the soil mass that decrease with depth due to spatial attenuation. This is shown in Figure 11 where Δp is plotted with respect to the p_o line that represents the existing geostatic stress distribution. As can been seen in Figure 11, Δp approaches the p_o line, which indicates that at a sufficient depth the effect of the externally imposed loads reduces significantly. In other words, this means that most of the strain due to the increased stress from the applied load will be experienced at relatively shallow depths below the load. As noted earlier, this depth is known as the depth of significant influence (DOSI), DS. Also, as indicated previously, DS depends on the load and load configuration as demonstrated by the pressure distribution charts in Section 4. Figure 11 also shows that that the final stress, p_f, in the soil mass at any depth is equal to p_o + Δp.

A chart such as that shown in Figure 11 is even more useful when the soil stratigraphy is plotted on it. Then the stress levels in various layers will be clearly identified, which can help the engineer determine depth of borings to collect subsurface information within DOSI as well as perform proper analysis.

Example 2 illustrates these concepts by providing calculations of pf with depth due to stress increments from a strip load and presenting the results of the calculations on a p_o-diagram.

6.0 Load-Deformation Process in Soils

When subjected to static and/or dynamic loads, soils deform mainly because of a change in void volume rather than through deformation of the soil solids. When the void volume decreases the soil is said to compress, consolidate, collapse or compact. There is an important distinction between these four mechanisms although conceptually they appear to be the same since each pertains to a reduction in volume.

• Compression: Compression is defined as a relatively rapid decrease in void volume that partially saturated (unsaturated) soils undergo as air is expelled from the voids during loading.
• Consolidation: Consolidation is generally defined as a time-dependent decrease in void volume that saturated and near-saturated soils undergo as water is expelled from the voids during loading.
• Collapse: Collapse is primarily related to soil structure and its response to an increase in water content that results in a rapid decrease in void volume. Collapse-susceptible soils characteristically have dry densities less than approximately 100 pcf (16 kN/m3) that suggest high void ratios. Their structure is like a honeycomb with fine-grained “bridges” connecting coarser-grained particles. When dry, these soils are able to sustain externally applied loads with very little deformation. However, upon being wetted they tend to undergo a rapid decrease in void volume as the fine-grained “bridges” lose strength and the entire structure collapses. The magnitude of the potential collapse increases with increasing load. One of the important things to note is that full saturation (S=100%) is not required for these types of soils to collapse. Often collapse occurs at a degree of saturation of 50 to 70%. Collapse-susceptible soils are very common in the southwest and midwest of the United States and in many other parts of the world.
• Compaction: Compaction is the name given to the compression that takes place generally under an impact-type loading (e.g., modified and standard Proctor), a static loading (e.g., rubber-tired or steel drum rollers) or kneading-type loading (e.g., sheepsfoot roller). Most commonly, the compaction processes are deliberate and intended to achieve a dense packing of soil particles. Regardless of the type of loading, the moisture content of the soil being compacted is far enough below the saturation moisture content that the compaction mechanism is considered to be related to compression (i.e., expulsion of air) rather than consolidation (i.e., expulsion of water) from the voids. Typically, the desired moisture content in the case of compaction is slightly above or below the PL. If the moisture content of the soil being compacted gets to be too close to the saturation moisture content then “pumping” will occur, i.e. water in addition to air will be forced out of the soil.

These distinctions in load-deformation processes should be kept in mind during the discussions that follow in subsequent sections of this course.

Finally, in contrast to the above processes that involve void volume decrease, there are conditions under which soils may actually increase in volume. When the void volume increases under static and/or dynamic load, the soil is said to dilate. Dilation can occur in either saturated or partially saturated soils. It is a function of the initial void ratio, confinement stress, and the magnitude and direction of the loading/unloading imposed on the soil. Expansion, on the other hand, is generally considered to be due to the presence of expansive clay minerals, such as montmorillonite (commercially known as “bentonite”), in the soil and the response of these minerals to the introduction of water into the void spaces. The physico-chemical properties of expansive clay minerals cause inter-particle repulsions to take place in the presence of water so that even under considerable externally applied loads these soils will undergo an increase in void volume that leads to swelling. A variation of the expansion is heave which can occur due to various factors such as frost action or reduction in overburden pressure due to excavation.

6.1 Time Dependent Load-Deformation (Consolidation) Process

Deformation of a saturated soil is more complicated than that of a dry soil since water, which fills the voids, must be squeezed out of the soil before readjustment of the soil grains can occur. The more permeable a soil is, the faster the deformation under load will occur. However, when the load on a saturated soil is quickly increased, the increase is initially carried by the pore water resulting in the buildup of an excess pore water pressure, ∆u. Excess pore water pressure is water pressure greater than the hydrostatic pressure. As drainage of the water takes place more and more load is gradually transferred from the pore water to the soil grains until the excess pore water pressure has dissipated completely and the soil grains readjust to a denser configuration under the applied load. This time dependent process is called consolidation and results in a decreased void ratio and greater unit weight relative to conditions before the load was applied. To illustrate this concept, one-dimensional (vertical) drainage of the water will be considered here. The process is analogous to loading a spring-supported piston in a cylinder filled with water. The spring-piston analogy is shown schematically in Figure 13 and is briefly discussed below.

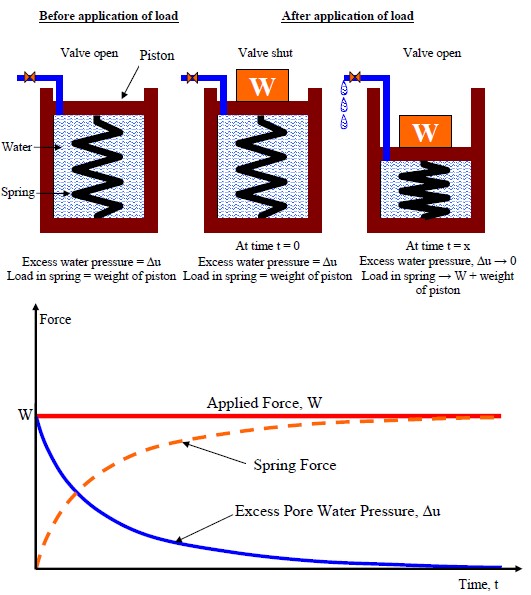
In the spring-piston model, the spring represents the solid phase of the soil and the water below the piston is the pore water under saturated condition in the soil mass. Before a new load, W, is applied to the piston, the system is assumed to be in equilibrium, i.e., the drainage valve is open and there is no excess pore water pressure, ∆u = 0. The spring alone is carrying any previously applied loads, such as the weight of the piston itself. The drainage valve is closed just before the new load is applied. If the valve is completely shut-off and the piston is leak-proof, then, there is no chance for water to escape. Such a condition represents a clay-water system in which the clay is very impermeable so that there is significant resistance to drainage of water in any direction. When the new load, W, is placed on the piston (this is called the initial or “time = 0” condition), the total applied pressure immediately below the piston, pt, which equals the load, W, divided by the area of the piston, is immediately transferred to the water. Since the drainage valve is closed and water is virtually incompressible, the water pressure increases to a value equal to the total applied pressure, i.e., the excess water pressure ∆u = p_t.

At “time = 0,” the spring does not carry any of the applied load W. The excess water pressure is analogous to the pore water pressure that would be developed in a clay-water system under externally applied loads, e.g., loads due to construction of an embankment on soft saturated clay. If the valve is now opened, the water will drain to relieve the excess pressure in it. With the escape of the water, a part of the pressure carried by the water is transferred to the spring where it induces a stress increase analogous to an effective increase in the inter-particle stresses, p_o, in a soil mass. The transfer of pressure from the water to the spring occurs over a period of time as shown on the bottom part of Figure 13, however, at any time during the process, the increased stress in the spring, p_o, plus the excess pressure in the water, ∆u, must equal the applied pressure, p_t. This transfer of pressure from the water to the spring goes on until the flow stops. At that time all of the applied pressure, p_t, will be carried by the spring, p_o, and none by the water, i.e., ∆u = 0, and the system will have come into equilibrium under the applied load. The time required to attain equilibrium depends on the avenue provided to the water to escape, i.e., the longest drainage path the water has to take to leave the system. In Figure 13 the longest drainage path is the length of the cylinder. Obviously, the system would drain quicker if there were another standpipe-type drain at the bottom of the cylinder.

Regardless of the number of avenues provided for drainage, the rate of excess water pressure drop generally decreases with time as shown in the lower half of Figure 13. After the spring water system attains an equilibrium condition under the imposed load, the compression of the piston is analogous to the settlement of the clay-water system under an externally applied load. This process is called consolidation.

6.2 Comparison of Drainage Rates between Coarse-Grained and Fine-Grained Soils

Figure 14 shows a comparison of excess pore water pressure dissipation in coarse-grained and fine-grained soils. The relatively large pore spaces in coarse-grained soils permit the water to drain quicker in comparison to fine-grained soils. This leads to a quick transfer of applied loads to the soil solids with an associated decrease in void space. This quick load transfer results in a displacement that is commonly termed “rapid” in contrast to the “long­term” displacement that is associated with the consolidation process in fine-grained soils.

7.0 Lateral Stresses in Foundation Soils

In most cases, the vertical stress at any depth in a soil mass due to its self weight is the summation of the simple products of the unit weight of each soil layer and its corresponding thickness down to the depth of interest. This vertical stress was denoted by p_t and the effective component of this pressure was denoted by p_o. Due a variety of factors, including depositional patterns, the lateral stress, p_h, in a soil mass is usually not the same as the vertical stress, p_o. Since the vertical stress is known with reasonable certainty for practical purposes, the lateral stress can be assumed to be a certain percentage of the vertical stress and can be expressed as follows:

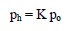
For an elastic solid, the value of the proportionality constant, K, can be expressed in terms of Poisson’s ratio, ν, as follows:

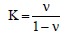
Poisson’s ratio, ν, is defined as a ratio of lateral to vertical strains. The value of Poisson’s ratio is a function of the type of material, e.g., ν is practically zero for cork (hence its suitability as a bottle stopper), for concrete ν is between 0.1 and 0.2, and for steel ν is between 0.27 and 0.30. A theoretical upper limit of Poisson’s ratio is 0.5 (rubber comes close to this limiting value). In the case of soils, ν will have a different value depending upon the type of soil and its moisture condition. For example, for free-draining soils a reasonable value of ν would be in the range of 0.25 to 0.35, while for very soft saturated clays under rapid loading conditions the value of ν would be close to 0.5. Thus, for free-draining soils, the value of K based on elasticity theory will range from 33% to 54% corresponding to ν=0.25 and ν=0.35, respectively, while for soft clays the value of K ≈ 1 since ν ≈ 0.5.

Even though a soil mass is not an elastic body, the point to be noted here is that at any point within the soil mass both vertical and horizontal (or lateral) stresses exist. When external forces are imposed on a soil mass, they will result in an increase in vertical stresses as discussed in Sections 5 and 6. Equation 14 indicates that an increase in vertical stresses will in turn lead to an increase in lateral stresses. While the increase in vertical stresses is important in assessing vertical settlements, change in lateral stresses may affect the load acting, for example, against piles supporting a bridge abutment, see Figure 15. In this figure, it can be seen that the increase in vertical stress imposed by the embankment leads to an increase in the lateral stress in the ground that causes lateral deformation (“squeeze”) of the soft soil. As the soft soil spreads laterally it will have an effect on foundations. Therefore, it is important to evaluate the increase in lateral stresses due to vertical loadings.

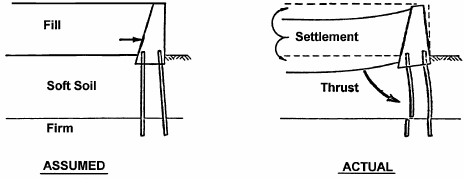
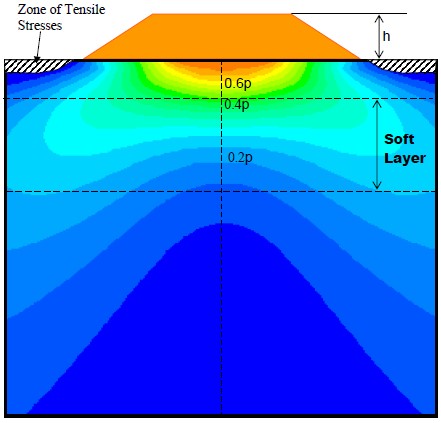
A two-dimensional (2-D) representation of the lateral stresses transverse to an embankment centerline is shown in Figure 16. This schematic was developed with a soft layer of soil under the embankment. It can be seen that significant lateral stresses are generated in the soil below the embankment load. Note that the vertical stresses due to the embankment can cause zones of tensile stresses to develop near the toes of the embankment as shown by the hatched zones in Figure 16. This means that tensile cracks are likely to develop near the toes of the embankments for this particular case. This knowledge can help the geotechnical specialist to select proper ground improvement measures rationally and to develop and implement an instrumentation program. The key point to understand based on the schematics shown in Figures 15 and 16 is that lateral deformations can be three-dimensional and can affect a number of facilities such as buried utilities, embankment slopes and bridge foundations. Lateral deformations can also affect off-site structures very easily leading to potential legal actions. The three-dimensional (3-D) lateral deformations coupled with vertical deformations due to vertical stresses can create a complex state of deformation that needs to be carefully considered in the design of geotechnical features.

Similar to the estimation of vertical stresses, the theory of linear elasticity yields equations for lateral stress distribution. However, in these equations Poisson’s ratio is assumed to be a constant. Hence, the use of chart solutions in these cases is not as simple as for the vertical stress case since complicated equations have to be evaluated (Poulos and Davis, 1974). One can prepare spreadsheet solutions based on the equations or use commercially available computer programs that have already programmed the equations. Program FoSSA (2003) by ADAMA Engineering (Version 1.0 was licensed to FHWA) is an example of a program capable of computing the vertical and lateral stresses due to surface loading, including embankment and multiple footings. Figures 10 and 16 were generated using the FoSSA program.

7.1 Effect of Shear Strength of Soils on Lateral Pressures

Up to now the stresses in soils have been explained by using unit weights and the theory of elasticity. Elastic theory, when suitably modified to reflect observed phenomena in soils, provides a tool to obtain a reasonable first approximation to a solution for many problems in geotechnical engineering. However, elastic theory does not recognize the role of shear strength of soil in the development of lateral pressures. For example, soils have an ability to stand vertically or at a certain slope. The reason for this observed ability is that soil has shear strength and to some degree can support itself. This shear strength may come from friction and/or cohesion between the soil particles. It is intuitive that these components of shear strength should also somehow affect the lateral pressures in soils computed by use of the theory of elasticity. The shear strength of soils and its representation for analytical purposes is discussed in the Section 8 followed in Section 9 by a demonstration of how the shear strength parameters can be used to express lateral pressures. Readers are referred to Lambe and Whitman (1979) or Holtz and Kovacs (1981) for detailed discussions.

8.0 Strength of Soils to Resist Imposed Stresses

If the imposed stress in a soil mass is increased until the deformations (movements) become unacceptably large, a “failure” is considered to have taken place. In this case, the strength of the soil is considered to be insufficient to withstand the applied stress.
The strength of geologic materials is a variable property that is dependent on many factors, including material properties, magnitude and direction of the applied forces and their rate of application, drainage conditions of the mass, and the magnitude of confining pressure. Unlike steel whose strength is usually discussed in terms of either tension or compression and concrete whose strength is generally discussed in terms of compressive strength only, the strength of soil is generally discussed in terms of shear strength. Typical geotechnical failures occur when the shear stresses induced by applied loads exceed the soil’s shear strength somewhere within the soil mass.

8.1 Basic Concept of Shearing Resistance and Shearing Strength

The basic concept of shearing resistance and shearing strength can be understood by first studying the principle of friction between solid bodies. Consider a prismatic block B resting on a plane surface XY as shown in Figure 17. The block B is subjected to two forces:

• A normal force, P_n, that acts perpendicular to the plane XY, and
• A tangential force, F_a, that acts parallel to the plane XY.

Assume that the normal force, P_n, is constant and that the tangential force, F_a, is gradually increased. At small values of F_a, the block B will not move since the applied force, F_a, will be balanced by an equal and opposite force, F_r, on the plane of contact XY. The resisting force, F_r, is developed as a result of surface roughness on the bottom of the block B and the plane surface XY. The angle, θ, formed by the resultant R of the two forces F_r and P_n with the normal to the plane XY is known as the angle of obliquity.

If the applied horizontal force, Fa, is gradually increased, the resisting force, F_r, will likewise increase, always being equal in magnitude and opposite in direction to the applied force. When the force Fa reaches a value that increases the angle of obliquity to a certain maximum value θ_m, the block B will start sliding along the plane. Recall that during this entire process the normal force, P_n, remains constant. The following terminology can now be developed:

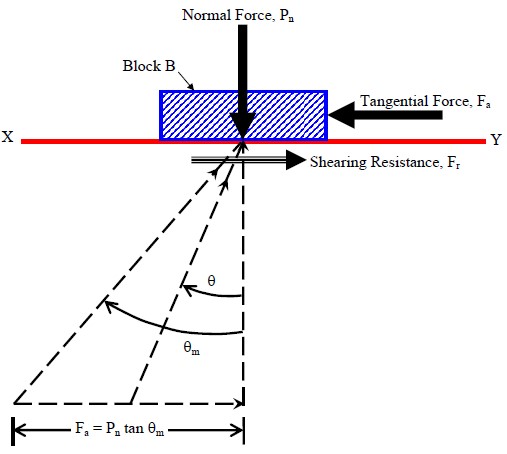
• If the block B and the plane surface XY are made of the same material, the angle θm is equal to φ, which is termed the angle of friction of the material. The value tan φ is called the coefficient of friction.
• If the block B and the plane surface XY are made of dissimilar materials, the angle θm is equal to δ, which is termed the angle of interface friction between the bottom of the block and the plane surface XY. The value tan δ is called the coefficient of interface friction.
• The applied horizontal force, Fa, on the block B is a shearing force and the developed force is called frictional resistance or shearing resistance. The maximum frictional or shearing resistance that the materials are capable of developing on the interface is (Fa)max.

If the same experiment is conducted with a greater normal force, P_n, the maximum frictional or shearing resistance (F_a)_max, will be correspondingly greater. A series of such experiments would show that for the case where the block and surface are made of the same material, the maximum frictional or shearing resistance is approximately proportional to the normal load P_n as follows:

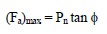
If A is the overall contact area of the block B on the plane surface XY, the relationship in Equation 2-16 may be written as follows to obtain stresses on surface XY:

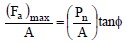
or

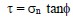
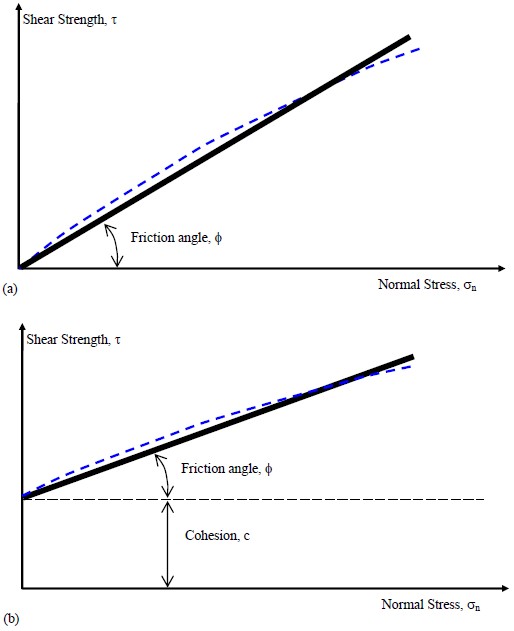
The term σn is called the normal stress and the term τ is called the shear strength. A graphical representation of Equation 18 is shown in Figure 18a. In reality, the relationship is curved, but since most geotechnical problems involve a relatively narrow range of pressures, the relationship is assumed to be linear as represented by Equation 18 over that range.

The concept of frictional resistance explained above applies to soils that possess only the frictional component of shear strength, i.e., generally coarse-grained granular soils. But soils that are not purely frictional exhibit an additional strength component due to some kind of internal electro-chemical bonding between the particles. This bonding between the particles is typically found in fine-grained soils and is termed cohesion, c. Simplistically, the shear strength, τ, of such soils is expressed by two additive components as follows and can be graphically represented as shown in Figure 18(b):

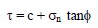
Again, in reality, the relationship is curved. But, as noted above, since most geotechnical problems involve a relatively narrow range of pressures, the relationship is assumed to be linear as represented by Equation 19 over that range.

Equation 19 was first proposed by French engineer Coulomb and is used to express shear strength of soils. When plotted on arithmetic axes the resulting straight line is conventionally known as the Mohr-Coulomb (M-C) failure envelope. “Mohr” is included in “Mohr-Coulomb” because Equation 19 can also be derived based on concept of Mohr’s circle. The development of the Mohr-Coulomb failure envelope based on the application of Mohr’s circle is presented in Appendix B.

As indicated previously, the deformation of soils occurs under effective stresses. In terms of effective stresses, Equation 19 can be re-written as follows:

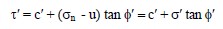
where c′ = effective cohesion, σ′ is the effective normal stress and φ′ is the effective friction angle.

In geotechnical engineering, the normal stresses are commonly expressed using the overburden pressure concept introduced in Section 3. In terms of overburden pressure, the term σn in above equations is the same as p_t and the term σ′ is the same as p_o. Thus, Equations 2-19 and 2­ 20 can be expressed in terms of overburden stresses as follows:

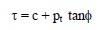
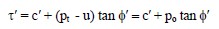
Since this course relates to geotechnical engineering, Equations 21 and 22 will be used to express the M-C failure envelope. The physical meaning of the M-C failure envelope shown in Figure 18(a) and Figure 18(b) may be explained as follows:

• Every point on the M-C failure envelope represents a combination of normal and shear stress that results in failure of the soil, i.e., the Mohr failure envelope essentially defines the strength of the soil. In other words, any point along the M-C envelope defines the limiting state of stress for equilibrium.
• If the state of stress is represented by a point below the M-C failure envelope then the soil will be stable for that state of stress.
• States of stress beyond the M-C failure envelope cannot exist since failure would have occurred before that point could be reached.

9.0 Strength of Soils Related to Lateral Earth Pressures

The concept of shear strength described in the previous section can now be used to understand the phenomenon of lateral earth pressure in a soil mass, which is related to problems of slope stability and earth retention. From a theoretical viewpoint, problems in these three areas (earth pressures, slope stability, and retaining structures) fall into a class of problems involving plasticity theory and are best solved by some form of equilibrium solution. Many geotechnical engineering text books (e.g., Lambe and Whitman, 1979; Holtz and Kovacs, 1981) deal with these solutions extensively. From a practical viewpoint, values of earth pressure are needed either directly or indirectly to determine:

1. If an unrestrained slope is stable and
2. If not, what kind of retaining structure will be required to stabilize the slope.

The simplest consideration of earth pressure theory starts with the assessment of the vertical geostatic effective stress, p_o, at some depth in the ground (effective overburden pressure) as considered in Section 3. The lateral geostatic effective stress, p_h, at this depth is given in general terms by Equation 14 where, for an ideally elastic solid, the value of the lateral earth pressure coefficient, K, is given by Equation 15. However, the behavior of real soils under loads is not always ideally elastic. To simplify the discussion of this topic, consider only dry coarse-grained cohesionless soils. The geostatic effective stress condition on a soil element at any depth, z, is shown in Figure 19a. Since the ground is “at-rest” without any external disturbance, this condition is commonly referred to as the “at-rest” condition with zero deformation. The coefficient of lateral earth pressure for this condition is labeled K_o.

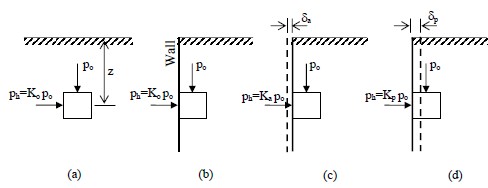
To relate to the lateral earth pressures acting on retaining structures, assume that a hypothetical, infinitely thin, infinitely rigid “wall” is inserted into the soil without changing the “at rest” stress condition in the soil. For the sake of discussion, assume that the hypothetical wall maintains the “at rest” stress condition in the soil to the right of the wall when the soil to the left of the wall is removed. This condition is shown in Figure 19b. Now suppose that the “at rest” condition is removed by allowing the hypothetical vertical wall to move slightly to the left, i.e., away from the soil element as shown in Figure 19c. In this condition, the vertical stress would remain unchanged. However, since the soil is cohesionless and cannot stand vertically on its own, it actively follows the wall. In this event, the horizontal stress decreases, which implies that the lateral earth pressure coefficient is less than K_o since the vertical stress remains unchanged. When this occurs the soil is said to be in the “active” state. The lateral earth pressure coefficient at this condition is called the “coefficient of active earth pressure,” Ka, and its value at failure is expressed in terms of effective friction angle, φ’, as follows:

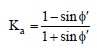
Returning to the condition shown in Figure 19b, now suppose that the “at rest” condition is removed by moving the hypothetical vertical wall to the right, i.e., into the soil element as shown in Figure 19d. Again, the vertical stress would remain unchanged. However, the soil behind the wall passively resists the tendency for it to move, i.e., the horizontal stress would increase, which implies that the lateral earth pressure coefficient would become greater than K_o since the vertical stress remains unchanged. When this occurs the soil is said to be in the “passive” state. The lateral earth pressure coefficient at this condition is called the “coefficient of passive earth pressure,” K_p, and its value at failure is expressed in terms of effective friction angle, φ’, as follows:

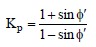
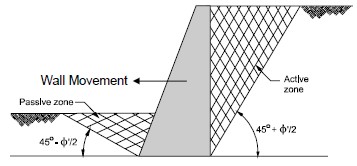
When failure occurs during either of the two processes described above, “Rankine” failure zones form within the soil mass. The details of how the failure zones develop are described in most geotechnical engineering textbooks and will not be treated here. The so-called “Rankine” failure zones and their angles from the horizontal are shown in Figure 20.

9.1 Distribution of Lateral Earth and Water Pressures

The earth pressure coefficients, K_a and K_p, can be substituted into Equation 14 to obtain equations for active and passive lateral earth pressures, respectively as follows:

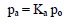
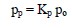
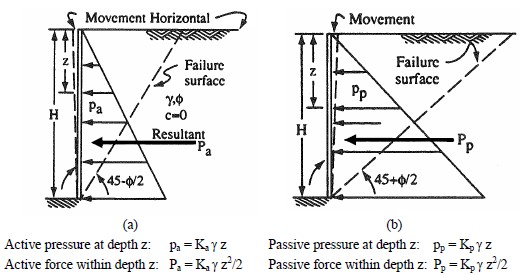
It can be seen from Equations 25a and 25b that the lateral pressures p_a and p_p are a certain fraction of the vertical effective overburden pressure p_o. Thus, active and passive lateral earth pressures are effective pressures and their distribution will be same as that for po. The overburden pressure increases in proportion to the unit weight and is typically triangular for a given geomaterial. The general distribution of the active and passive pressures along with the configuration of active and passive failure surfaces is shown in Figure 21a and 21b, respectively.

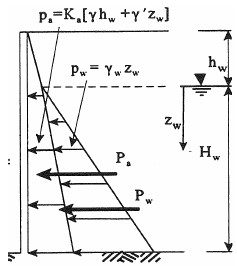
In cases where ground water exists, the lateral pressure due to the water at any depth below the ground water level is equal to the hydrostatic pressure at that point since the friction angle of water is zero and use of either Equation 23 or 24 leads to a coefficient of lateral pressure for water, K_w equal to 1.0. The computation of the vertical water pressure was demonstrated previously in Example 1. Since Kw=1, the same computation applies for the lateral pressure as well. The lateral earth pressure is computed by using the vertical effective overburden pressure p_o at any depth and applying Equations 25a and 25b. The lateral earth pressure is added to the hydrostatic water pressure to obtain the total lateral pressure acting on the wall at any point below the ground water level. For a typical soil friction angle of 30 degrees, K_a = 1/3. Since K_w = 1, it can be seen that the lateral pressure due to water is approximately 3 times that due the active lateral earth pressure. A general case for the distribution of combined active lateral earth pressure and lateral water pressure is shown in Figure 22. This disparity in lateral pressures has serious consequences when the stability of walls is considered and is the reason why drainage behind walls is so important.

9.2 Deformations Associated with Lateral Pressures

The active and passive pressures are predicated on the development of a certain amount of lateral deformation in the soil.

10.0 Unsaturated Soil Mechanics

As discussed in this course, soil is three phase system that consists of solid particles, liquid and gas. Classical soil mechanics concentrates primarily on the behavior of saturated or dry soils, i.e., a two phase system. For soils in a saturated state, the principle of effective stress is invoked to quantify stress and strain in the soil mass. For soils in a dry state, pore water pressure does not exist and the total stress and effective stress are the same. In reality, all the pore space in soil within the depth of significant influence of geotechnical features is rarely occupied by liquid or gas alone. This is particularly true for soils above the ground water table and soils that are mechanically compacted as in the case of earthworks. In such soils the degree of saturation is generally intermediate between 0% (dry soil) and 100% (saturated soil). Under these conditions, negative pore pressures, i.e., suction, may exist within the soil mass depending upon the type of soil and its grain size distribution. An example of the presence of negative pore pressures is the capillary rise often encountered above the water table. Such negative pore pressures affect all aspects of soil behavior ranging from volume change and shear strength to seepage. Consequently, unsaturated soil behavior impacts a broad array of engineering issues ranging from foundation design and performance to flow through earth embankments and the engineering of facilities on or in expansive, collapsible and compacted soils (ASCE 1993, 1997).

To date the tendency in engineering practice has often been to apply a total stress approach where the effects of negative pore pressures are not properly simulated. In the last couple of decades significant progress has been made to model such negative pore pressures and that field of study is often called “unsaturated soil mechanics.” Discussion of the engineering behavior of unsaturated soils is beyond the scope of this course. At this stage, it is important simply to realize that advanced studies beyond those discussed in this course may be required on projects where unsaturated state can significantly affect the engineering behavior of soils. The interested readers are directed to the work by Fredlund and Rahardjo (1993), who provide a comprehensive treatment of unsaturated soils.